Thi và Đua xuất phát từ A đến B cùng 1 lúc. Thi đi nửa quãng đường đầu với vận tốc 5 km/giờ, nửa quãng đường còn lại với vận tốc 4km/giờ.Đua đi nửa thời gian đầu với vận tốc 5km/giờ, nửa thời gian còn lai với vận tốc 4km/giờ.Hỏi ai đến B trước?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
22 tháng 5 2019
Giả sử quãng đường AB dài a km
Thi đi quãng đường \(\frac{a}{2}\)với vận tốc 5 km/giờ và quãng đường \(\frac{a}{2}\)với vận tốc 4 km/giờ. Nên:
Thời gian Thi đi nửa quãng đường đầu là:
\(\frac{a}{2}\):5=\(\frac{a}{10}\)(giờ)
Thời gian Thi đi nửa quãng đường còn lại là:
\(\frac{a}{2}\):4=\(\frac{a}{8}\)(giờ)
Tổng thời gian Thi đi từ A đến B là:
\(\frac{a}{10}\)+\(\frac{a}{8}\)=\(\frac{a.9}{40}\)(giờ)
Hai nửa thời gian thì bằng nhau và thời gian không đổi thì quãng đường tỉ lệ thuận với vận tốc.Nên:
Nửa thời gian đầu Đua đi được 5 phần quãng đường thì nửa thời gian còn lại Đua đi được 4 phần quãng đường như thế. Tức là nửa thời gian đầu Đua đi được \(\frac{5}{9}\)đoạn đường AB.
Nửa thời gian Đua đi từ A đến B là:
\(\frac{a.5}{9}\):5=\(\frac{a}{9}\)(giờ)
Tổng thời gian Đua đi từ A đến B là:
\(\frac{a}{9}\). 2=\(\frac{a.2}{9}\)(giờ)
Để so sánh thời gian của Thi với Đua, ta so sánh 2 phân số \(\frac{9}{40}\)và\(\frac{2}{9}\)
Vì: \(\frac{9}{40}\)>\(\frac{2}{9}\)nên thời gian Thi đi lớn hơn thời gian Đua đi. Vậy Đua tới B trước.
CM
28 tháng 5 2017
Ta xét một đoạn đường cụ thể. Giả sử đoạn AB là 20 km thì nửa đoạn đường sẽ là:
20: 2 = 10 (km).
Thời gian An đi nửa đoạn đường đầu là:
10: 5 = 2 (giờ).
Thời gian An đi nửa đoạn đường sau là:
10: 4 = 2 giờ 30 phút.
Tổng thời gian An đi là:
2 giờ + 2 giờ 30 phút = 4 giờ 30 phút.
Vận tốc trung bình của An là:
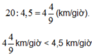
Hai nửa thời gian bằng nhau nên nếu Bình đi 1 giờ với vận tốc 5 km/giờ thì cũng đi 1 giờ với vận tốc 4 km/giờ nên vận tốc trung bình của Bình là:
(4 + 5): 2 = 4,5 (km/giờ).
Hai người đi đoạn đường bằng nhau mà bạn Bình có vận tốc trung bình lớn hơn nên tới B trước.
Nhi Trần Lê Uyển
Hai người đến B cùng một lúc
bạn có thể giải ko