Cho hai hàm số sau y = x + 1 và y = – 2x + 4 a/ Vẽ trên cùng một mặt phẳng tọa độ đồ thị hai hàm số trên. b/ Tìm tọa độ giao điểm của hai hàm số đó. c/ Tính khoảng cách từ gốc tọa độ đến đường thẳng y = – 2x + 4 (kết quả làm tròn đến chữ số thập phân thứ 3) ( chỉ mình câu c với ạ mình k bt làm câu này giúp với ạ )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+1=-2x+4\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)

b: Tọa độ là:
\(\left\{{}\begin{matrix}x+1=-2x+4\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}3x=-x+4\\y=3x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)
c: Gọi A,B lần lượt là giao điểm của đường thẳng y=-x+4 đến hai trục Ox, Oy
Tọa độ điểm A là: \(\left\{{}\begin{matrix}y_A=0\\4-x=0\end{matrix}\right.\Leftrightarrow A\left(4;0\right)\)
Tọa độ điểm B là: \(\left\{{}\begin{matrix}x_A=0\\y=-0+4=4\end{matrix}\right.\Leftrightarrow B\left(0;4\right)\)
\(AB=\sqrt{\left(0-4\right)^2+\left(4-0\right)^2}=4\sqrt{2}\)
Khoảng cách từ O đến đường thẳng y=-x+4 là:
\(AH=\dfrac{OA\cdot OB}{AB}=\dfrac{16}{4\sqrt{2}}=2\sqrt{2}\)
Tọa độ giao điểm là:
{3x=−x+4y=3x⇔{x=1y=3{3x=−x+4y=3x⇔{x=1y=3
c: Gọi A,B lần lượt là giao điểm của đường thẳng y=-x+4 đến hai trục Ox, Oy
Tọa độ điểm A là: {yA=04−x=0⇔A(4;0){yA=04−x=0⇔A(4;0)
Tọa độ điểm B là: {xA=0y=−0+4=4⇔B(0;4){xA=0y=−0+4=4⇔B(0;4)
AB=√(0−4)2+(4−0)2=4√2AB=(0−4)2+(4−0)2=42
Khoảng cách từ O đến đường thẳng y=-x+4 là:
AH=OA⋅OBAB=164√2=2√2

b: Tọa độ giao là:
2x+5=x+3 và y=x+3
=>x=-2 và y=1
c: Thay x=-2 và y=1 vào (d), ta được:
m-3-6=1
=>m=10

a: 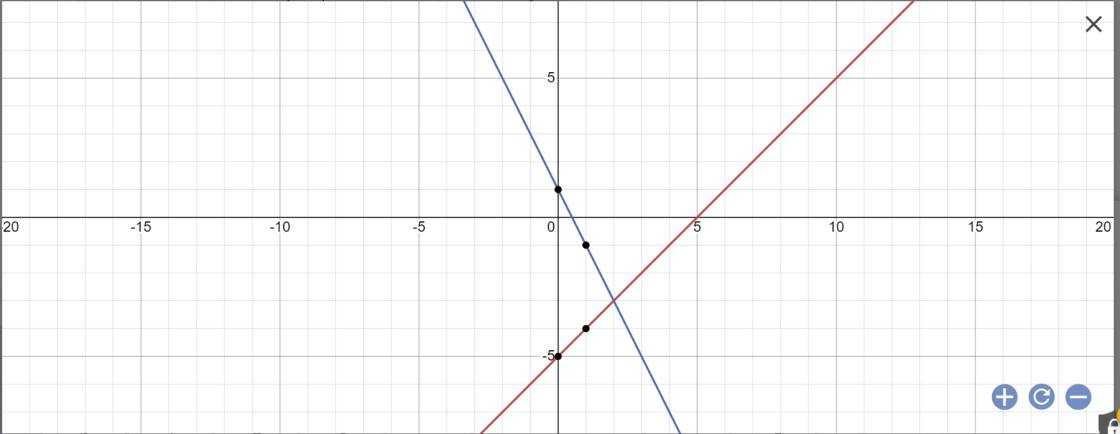
b: Phương trình hoành độ giao điểm là:
-2x+1=x-5
=>-2x-x=-5-1
=>-3x=-6
=>x=2
Thay x=2 vào y=x-5, ta được:
\(y=2-5=-3\)
Vậy: (d1) cắt (d2) tại A(2;-3)
c: (d1): y=x-5
=>x-y-5=0
Khoảng cách từ O(0;0) đến (d1) là:
\(d\left(O;\left(d1\right)\right)=\dfrac{\left|0\cdot1+0\cdot\left(-1\right)-5\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{5}{\sqrt{2}}\)
(d2): y=-2x+1
=>y+2x-1=0
=>2x+y-1=0
Khoảng cách từ O đến (d2) là:
\(d\left(O;\left(d2\right)\right)=\dfrac{\left|0\cdot2+0\cdot1-1\right|}{\sqrt{2^2+1^2}}=\dfrac{1}{\sqrt{5}}\)

b. PTHĐGĐ của hai hàm số:
\(x+2=-2x+1\)
\(\Rightarrow x=-\dfrac{1}{3}\)
Thay x vào hs đầu tiên: \(y=-\dfrac{1}{3}+2=\dfrac{5}{3}\)
Tọa độ điểm \(A\left(-\dfrac{1}{3};\dfrac{5}{3}\right)\)
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x+2=-2x+1\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\y=\dfrac{5}{3}\end{matrix}\right.\)
c: Gọi A,B lần lượt là tọa độ giao điểm của đường thẳng y=-2x+4 đến trục Ox, Oy
Tọa độ điểm A là:
\(\left\{{}\begin{matrix}y_A=0\\-2x+4=0\end{matrix}\right.\Leftrightarrow A\left(2;0\right)\)
Tọa độ điểm B là:
\(\left\{{}\begin{matrix}x_B=0\\y_B=-2\cdot0+4\end{matrix}\right.\Leftrightarrow B\left(0;4\right)\)
Gọi OH là khoảng cách từ O đến đường thẳng y=-2x+4
Xét ΔOAB vuông tại O có OH là đường cao
nên \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}\)
hay \(OH=\dfrac{4\sqrt{5}}{5}\left(cm\right)\)