cho hình chóp SABCD có M thuộc SC.
a)tìm giao điểm của AM với mặt phẳng(AMN)
b)N thuộc BC.tìm giao điểm của SD và mặt phẳng (AMN)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 6 2017
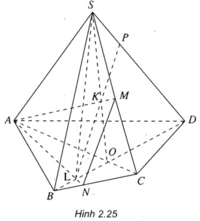
Gọi
O = AC ∩ BD
K = SO ∩ AN
L = BD ∩ AN
P = KL ∩ SD
Ta có P = SD ∩ (AMN).
Nhận xét: Trong cách giải trên, ta lấy (SBD) là mặt phẳng chứa SD, rồi tìm giao tuyến của (SBD) với (AMN). Từ đó tìm giao điểm của giao tuyến này và SD.
CM
7 tháng 11 2019
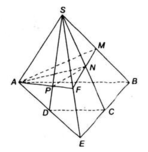
a) Tìm (SAD) ∩ (SBC)
Gọi E= AD ∩ BC. Ta có:
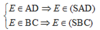
Do đó E ∈ (SAD) ∩ (SBC).
mà S ∈ (SAD) ∩ (SBC).
⇒ SE = (SAD) ∩ (SBC)
b) Tìm SD ∩ (AMN)
+ Tìm giao tuyến của (SAD) và (AMN) :
Trong mp (SBE), gọi F = MN ∩ SE :
F ∈ SE ⊂ (SAD) ⇒ F ∈ (SAD)
F ∈ MN ⊂ (AMN) ⇒ F ∈ (AMN)
⇒ F ∈ (SAD) ∩ (AMN)
⇒ AF = (SAD) ∩ (AMN).
+ Trong mp (SAD), gọi AF ∩ SD = P
⇒ P = SD ∩ (AMN).
c) Tìm thiết diện với mp(AMN):
(AMN) ∩ (SAB) = AM;
(AMN) ∩ (SBC) = MN;
(AMN) ∩ (SCD) = NP
(AMN) ∩ (SAD) = PA.
⇒ Thiết diện cần tìm là tứ giác AMNP.
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 7 2021
Miền trong tam giác SC và gì nữa bạn? Tam giác phải có 3 đỉnh
31 tháng 3 2017
a) (SAD) ∩ (SBC) = SE
b) Trong (SBE): MN ∩ SE = F
Trong (SAE): AF ∩ SD = P là điểm cần tìm
c) Thiết diện là tứ giác AMNP
30 tháng 10 2023
a: Xét ΔSBD có
M,N lần lượt là trung điểm của SB,SD
=>MN là đường trung bình
=>MN//BD
BD//MN
\(MN\subset\left(AMN\right)\)
BD không thuộc mp(AMN)
Do đó: BD//(AMN)
b: Gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Chọn mp(SBD) có chứa MN
(SBD) giao (SAC)=SO(cmt)
Gọi K là giao điểm của SO với MN
=>K là giao điểm của MN với mp(SAC)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 8 2023
a) Ta có: AM cắt CD tại E nên E thuộc (AMN) và (SCD)
Mà N thuộc (AMN) và (SCD)
Do đó: EN là giao tuyến của hai mặt phẳng cần tìm.
b) Ta có: En cắt SC tại F nên F thuộc (AMN) và (SBC)
Mà M thuộc (AMN) và (SBC)
Do đó: FM là giao tuyến của hai mặt phẳng cần tìm.