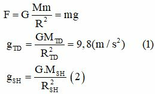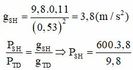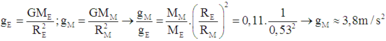Dùng công thức gia tốc trọng trƣờng g = GM/R2 . Tìm gia tốc trọng trƣờng gH trên sao Hỏa biết khối lƣợng sao Hỏa bằng 0,5325 bán kính Trái Đất, theo đơn vị m/s2 . Biết gia tốc trọng trƣờng Trái Đất gTĐ = 9,8 m/s2
A. 1,204 B. 0,305 C. 3,712 D. 6,218
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TM
0
VT
19 tháng 9 2019
Từ đầu bài, ta có:
M S H = 0 , 1 M T D R S H = 0 , 53 R T D và gia tốc trọng trường trên mặt đấtg=9,8m/s2
Áp dụng biểu thức tính gia tốc trọng trường ta có:
Gia tốc trọng trường trên mặt đất
g = G M T D R T D 2 1
Gia tốc trọng trường trên sao Hỏa
g S H = G M S H R S H 2 2
Lấy 1 2 ta được:
g g S H = M T D R S H 2 M S H R T D 2 = M T D .0 , 53 2 R T D 2 0 , 1 M T D . R T D 2 = 2 , 809 → g S H = g 2 , 809 = 9 , 8 2 , 809 = 3 , 49 m / s 2
Đáp án: A
VT
26 tháng 8 2019
Ta có F = G M m R 2 = m g
Khi ở trên Trái Đất g T D = G . M T D R T D 2 = 9 , 8 ( m / s 2 ) ( 1 )
Khi ở trên Sao Hỏa g S H = G . M S H R S H 2 ( 2 )
Từ (1) và (2) ta có: g S H = 9 , 8.0 , 11 0 , 53 2 = 3 , 8 ( m / s 2 )
Ta có P S H P T D = g S H g T D ⇒ P S H = 600.3 , 8 9 , 8 = 232 , 653 N
VT
21 tháng 7 2018
Chọn đáp án C
+ Gia tốc rơi tự do trên sao Hỏa: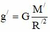 
+ Gia tốc rơi tự do trên mặt đất: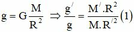 
+ Theo đề:
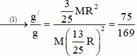
= 4,44 m/
s
2
30 tháng 11 2021
Tại mặt đất: \(g_0=G\cdot\dfrac{M}{R^2}\)
Tại Sao Hỏa: \(g=G\cdot\dfrac{M}{R^2}\)
Ta xét tỉ lệ:
\(\dfrac{g_0}{g}=\dfrac{M\cdot0,53^2R^2}{0,1M\cdot R^2}=2,809\)
\(\Rightarrow g=\dfrac{9,8}{2,809}=3,5\)m/s2
VT
30 tháng 1 2019
Từ đầu bài, ta có:
M S H = 0 , 1 M T D R S H = 0 , 53 R T D
và gia tốc trọng trường trên mặt đất g=9,8m/s2
Áp dụng biểu thức tính gia tốc trọng trường ta có:
Gia tốc trọng trường trên mặt đất:
g = G M R T D 2 1
Gia tốc trọng trường trên sao Hỏa
g S H = G M S H R S H 2 2
Lấy 1 2 ta được:
g g S H = M T D R S H 2 M S H R T D 2 = M T D .0 , 53 2 R T D 2 0 , 1 M T D . R T D 2 = 2 , 809 → g S H = g 2 , 809 = 9 , 8 2 , 809 = 3 , 49 m / s 2
Đáp án: A
14 tháng 12 2016
bán kính của sao hỏa là R1 còn của trái đất là R
Khối lượng trái đất là M, sao hỏa là M1, gia tốc rơi tự do ở sao hỏa là g1
gia tốc rơi tự do ở trái đất là g= \(\frac{GM}{R^2}\)
gia tốc rơi tự do ở sao hỏa là g1= \(\frac{GM_1}{R_1^2}\) = \(\frac{G.0,11M}{0,53^2_{ }R^2}\)
lập tỉ số giữa g và g1
kết quả g1 gần bằng 3,9 m/s2