B = sin2 230 + + sin2670 – cos600
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn A.
Vì 300 và 600 là hai góc phụ nhau nên 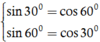
Suy ra: P = sin300.cos600 + cos300.sin600 = cos600.cos600 + sin600.cos600 = 1.

Chọn D.
Vì 300 và 600 là hai góc phụ nhau nên 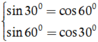
Do đó: P = cos300.cos600 - sin300.sin600 = cos300.cos600 - cos300.cos600 = 0.


\(S_{HKE}=S_{ABC}-S_{AKE}-S_{BHE}-S_{CHK}\)
\(\Leftrightarrow\dfrac{S_{HKE}}{S_{ABC}}=1-\dfrac{S_{AKE}}{S_{ABC}}-\dfrac{S_{BHE}}{S_{ABC}}-\dfrac{S_{CHK}}{S_{ABC}}\)
\(\Leftrightarrow\dfrac{1}{4}=1-\dfrac{\dfrac{1}{2}AE.AK.sinA}{\dfrac{1}{2}AB.AC.sinA}-\dfrac{\dfrac{1}{2}BH.BE.sinB}{\dfrac{1}{2}AB.BC.sinB}-\dfrac{\dfrac{1}{2}CH.CK.sinC}{\dfrac{1}{2}AC.BC.sinC}\)
\(\Leftrightarrow\dfrac{AE.AK}{AB.AC}+\dfrac{BH.BE}{AB.BC}+\dfrac{CH.CK}{AC.BC}=\dfrac{3}{4}\)
(Để ý rằng \(\dfrac{AE}{AC}=cosA\) do tam giác ACE vuông tại E và tương tự...)
\(\Leftrightarrow cosA.cosA+cosB.cosB+cosC.cosC=\dfrac{3}{4}\)
\(\Leftrightarrow cos^2A+cos^2B+cos^2C=\dfrac{3}{4}\)
\(\Leftrightarrow1-sin^2A+1-sin^2B+1-sin^2C=\dfrac{3}{4}\)
\(\Leftrightarrow sin^2A+sin^2B+sin^2C=\dfrac{9}{4}\)

\(\dfrac{1+cos2a-sin2a}{1+cos2a+sin2a}=\dfrac{2cos^2a-2sina.cosa}{2cos^2a+2sinacosa}\)
\(=\dfrac{2cosa\left(cosa-sina\right)}{2cosa\left(cosa+sina\right)}=\dfrac{cosa-sina}{cosa+sina}=\dfrac{\sqrt{2}sin\left(\dfrac{\pi}{4}-a\right)}{\sqrt{2}cos\left(\dfrac{\pi}{4}-a\right)}=tan\left(\dfrac{\pi}{4}-a\right)\)
\(\dfrac{1+cos2a-cosa}{sin2a-sina}=\dfrac{2cos^2a-cosa}{2sina.cosa-sina}=\dfrac{cosa\left(2cosa-1\right)}{sina\left(2cosa-1\right)}=\dfrac{cosa}{sina}=cota\)

Sử dụng 2 công thức: \(sina=cos\left(90^0-a\right)\) và \(sin^2a+cos^2a=1\) ta có:
\(A=sin^25^0+cos^2\left(90^0-85^0\right)=sin^25^0+cos^25^0=1\)

\(cos^2\left(a-b\right)-sin^2\left(a+b\right)\)
\(=\left(cosa.cosb+sina.sinb\right)^2-\left(sina.cosb+cosa.sinb\right)^2\)
\(=cos^2a.cos^2b+sin^2a.sin^2b-sin^2a.cos^2b-cos^2a.sin^2b\)
\(=cos^2b\left(cos^2a-sin^2a\right)-sin^2b\left(cos^2a-sin^2a\right)\)
\(=\left(cos^2b-sin^2b\right)\left(cos^2a-sin^2a\right)\)
\(=cos2a.cos2b\left(dpcm\right)\)

\(B=1-\dfrac{1}{2}+\dfrac{3}{2}=1+1=2\)