Cho tam giác abc có diện tích =600 cm2 d là trung điểm của cạnh bc. Trên ac lấy điểm e sao cho ae=1/3ac. ab cắt be tại m. Tính diện tích ame ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 12 2019
S(BDM) = S(CDM) => S(ABM) = S(ACM) S(AEM) = 1/2 S(CEM) => S(ABM) = 1/2 S(BCM) mà S(BDM) = S( CDM) => S(ABM) = S(BDM) = S( CDM) = S(ACM) = 600 : 4 = 150 c m 2 => S(AEM) = 150 : (1+2) = 50 c m 2
LA
4 tháng 2 2017
Ta có:
SAME = 1/3 SAMC
Mà SAMC = SAMB (Vì SBMD = SCMD và SABD = SACD)
=> SAME = 1/4 SABE (1)
Mà SABE = 1/3 SABC (2)
Từ (1) và (2) => SAME = (1/4 x 1/3) SABC = 1/12 SABC = 600 :12 = 50 cm2
23 tháng 3 2016
Ta có:
SAME = 1/3 SAMC
Mà SAMC = SAMB (Vì SBMD = SCMD và SABD = SACD)
=> SAME = 1/4 SABE (1)
Mà SABE = 1/3 SABC (2)
Từ (1) và (2) => SAME = (1/4 x 1/3) SABC = 1/12 SABC = 600 :12 = 50 cm2
CM
3 tháng 3 2019
(BDM) = S(CDM)
=> S(ABM) = S(ACM)
S(AEM) = 1/2 S(CEM)
=> S(ABM) = 1/2 S(BCM)
mà S(BDM) = S( CDM)
=> S(ABM) = S(BDM) = S( CDM) = S(ACM) = 600 : 4 = 150 cm2
=> S(AEM) = 150 : (1+2) = 50 cm2
CH
Cô Hoàng Huyền
Admin
VIP
7 tháng 3 2018
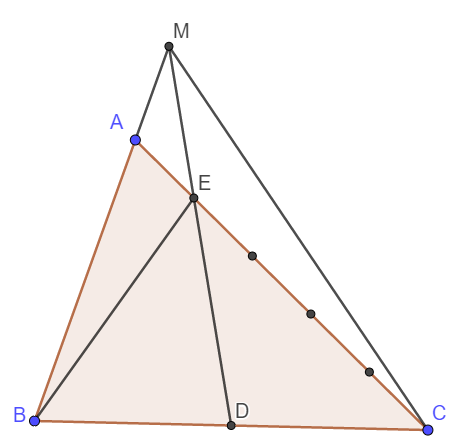
a) Ta thấy ngay tam giác MAE và tam giác MEC có chung chiều cao hạ từ M xuống AC, EC = 4AE nên \(S_{MEC}=4S_{MAE}=4\times20=80\left(cm^2\right)\)
b) Ta thấy tam giác MBD và tam giác MCD có chung chiều cao và đáy BD = DC nên \(S_{MBD}=S_{MCD}\)
Ta thấy tam giác EBD và tam giác ECD có chung chiều cao và đáy BD = DC nên \(S_{EBD}=S_{ECD}\)
Vậy nên \(S_{MBE}=S_{MEC}=80\left(cm^2\right)\)
Ta có \(\frac{S_{AME}}{S_{MEC}}=\frac{1}{4};\frac{S_{ABE}}{S_{EBC}}=\frac{1}{4}\Rightarrow\frac{S_{AME}+S_{ABE}}{S_{MEC}+S_{EBC}}=\frac{1}{4}\Rightarrow\frac{S_{MBE}}{S_{MEBC}}=\frac{1}{4}\)
\(\Rightarrow S_{MEBC}=4.80=320\left(cm^2\right)\)
\(\Rightarrow S_{MBC}=320+80=400\left(cm^2\right)\)
\(\Rightarrow S_{ABC}=400-20-80=300\left(cm^2\right)\)
oh ! mk cũng thik hc hình nhưng thông cảm phải vẽ hình ra mk mới làm đc