Nêu cách chia một tứ giác lồi bất kì thành 2 phần có diện tích bằng nhau. Giải thích cách làm nếu được (tức là chứng minh)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chia đoạn thẳng BC thành 3 phần bằng nhau rồi nối chúng tới A (như hình vẽ). Bởi chúng sẽ có chung đáy và chiều cao.
Mình nghĩ là cần kẻ 2 đoạn thẳng còn làm 1 đoạn thì mình chịu

Ta sẽ dùng phản chứng
Gọi 4 cạnh của tứ giác là a , b , c , d ( a,b,c,d \(\inℕ^∗\))
Giả sử không có bất kì 2 cạnh nào bằng nhau
Đặt \(\hept{\begin{cases}x=\frac{b+c+d}{a}\\y=\frac{c+d+a}{b}\\z=\frac{d+a+b}{c}\end{cases}}\left(x;y;z\inℕ^∗\right)\)(Do tổng 3 cạnh bất kì chia hết cho cạnh còn lại)
Theo bất đẳng thức trong tứ giác thì dễ thấy \(x;y;z>1\)
Mà x,y,z là số tự nhiên nên \(x;y;z\ge2\)
Không mất tính tổng quát của bài toán ta giả sử a > b > c > d thì khi đó x < y < z
Ta có : \(\hept{\begin{cases}x\ge2\\y>x\end{cases}}\Rightarrow y\ge3\)
tương tự : \(z\ge4\)
Từ điều giả sử\(\Rightarrow\) \(\hept{\begin{cases}b+c+d\ge2a\\c+d+a\ge3b\\d+a+b\ge4c\end{cases}}\)
Cộng 3 vế vào ta được \(2a+2b+2c+3d\ge2a+3b+4c\)
\(\Rightarrow3d\ge b+2c\)(Vô lí do b > c > d)
Nên điều giả sử là sai
Vậy luôn tồn tại ít nhất 2 cạnh bằng nhau trong tứ giác đó

ta có diện tích hai tam giác AFE bằng BFE ( do tam giác ABF có đường trung tuyến FE)
kết hợp với giả thiết ta có diện tích ADF bằng BCF
hay d(A,DF).DF.1/2=d(B,CF).CF.1/2
hay d(A,DF)=d(B,CF)d(A,DF)=d(B,CF) hay AB song song với DC
vậy => đpcm
Thông cảm , hình ko cho vẽ
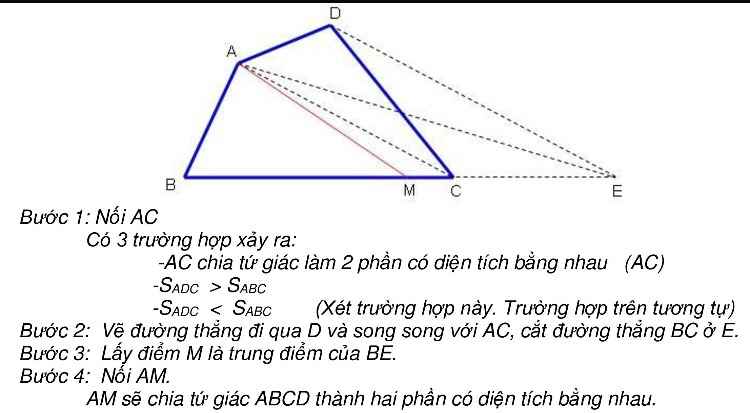
Bước 1 : Nối AC
Có 3 trường học xảy ra :
- AC chia tứ giác làm 2 phần diện tích bằng nhau ( AC)
\(-Sadc>Sabc\)
\(-Sadc< Sabc\)
( Xét trường hợp này trường hợp tương tự )
Bước 2 : Vẽ đường thẳng qua D và song song với AC , cắt đường BC ở E .
Bước 3 : Lấy M đi qua trung điểm của BE
Bước 4 : Nối AM
AM sẽ chia tứ giác ABCD thành hai phần có diện tích bằng nhau