Bài 5 :(3,5 điểm) Cho tam giác ABC có AB = AC, M là trung điểm của BC. Trên tia đối
của tia MA lấy điểm E sao cho ME = MA. Chứng minh rằng:
a) tam giác ABM = tam giác ACM; b) AB //CE; c) AM vuông góc BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 12 2021
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
15 tháng 12 2023
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
b: Xét ΔMBA vuông tại M và ΔMCD vuông tại M có
MB=MC
MA=MD
Do đó: ΔMBA=ΔMCD
=>\(\widehat{MBA}=\widehat{MCD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
c: Xét ΔBEM vuông tại E và ΔCFM vuông tại F có
MB=MC
\(\widehat{MBE}=\widehat{MCF}\)
Do đó: ΔBEM=ΔCFM
=>ME=MF
ΔBEM=ΔCFM
=>\(\widehat{BME}=\widehat{CMF}\)
mà \(\widehat{BME}+\widehat{EMC}=180^0\)(hai góc kề bù)
nên \(\widehat{CMF}+\widehat{EMC}=180^0\)
=>F,M,E thẳng hàng
mà MF=ME
nên M là trung điểm của EF
20 tháng 7 2023
a)xet ΔABM vaΔECM co:
AM=EM(GT)
∠AMB = ∠EMC(doi dinh)
BM=CM(M la trung diem BC)
⇒ΔABM =ΔECM(g.c.g)
b)Theo cau a co:ΔABM =ΔECM
⇒AB = CE ( 2 canh tuong ung)
(O DAY LA AC//BE HAY AB//EC HA BAN?)
5 tháng 1 2022
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
DO đó: ΔABM=ΔACM
b: Xét ΔABM và ΔDCM có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔABM=ΔDCM
Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB//DC
TA
20 tháng 7 2023
a) Xét tam giác ABM và tam giác ECM
Có:
AM = EM (gt)
BM = MC (gt)
AE cạnh chung
=> Tam giác ABM = tam gicas ECM (c.c.c)
b) Ta có: Tam giác ABM = tam giác ECM
=> AB = Ce (2 cạnh t/ư)
Tiếp theo bạn kẻ thêm rồi xét 2 tam giác ACM và tam giác BME (tương tự như câu A th) nhé (cả hình giống hình thoi nhé)
Từ đó có tam giác ACM = tam giác BME
=> Góc AMC = góc BME (2 góc đối đỉnh)
=> AC//BE (đpcm)
:))
21 tháng 7 2023
a: Xét ΔABM và ΔECM có
MA=ME
góc AMB=góc EMC
MB=MC
=>ΔABM=ΔECM
b: ΔABM=ΔECM
=>AB=CE
Xét tứ giác ABEC có
M là trung điểm chung của AE và bC
=>ABEC là hình bình hành
=>AC//BE
4 tháng 1 2022
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
DO đó: ABDC là hình bình hành
Suy ra: AB//CD
26 tháng 12 2023
a: Xét ΔMAB và ΔMEC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMEC
b: Ta có: ΔMAB=ΔMEC
=>AB=EC
Ta có: ΔMAB=ΔMEC
=>\(\widehat{MAB}=\widehat{MEC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CE
c: Xét ΔMAC và ΔMEB có
MA=ME
\(\widehat{AMC}=\widehat{EMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMEB
=>\(\widehat{MAC}=\widehat{MEB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BE
d: Xét ΔIAM và ΔKEM có
IA=KE
\(\widehat{IAM}=\widehat{KEM}\)
AM=EM
Do đó: ΔIAM=ΔKEM
=>\(\widehat{IMA}=\widehat{KME}\)
mà \(\widehat{IMA}+\widehat{IME}=180^0\)(hai góc kề bù)
nên \(\widehat{KME}+\widehat{IME}=180^0\)
=>I,M,K thẳng hàng
14 tháng 1
a:
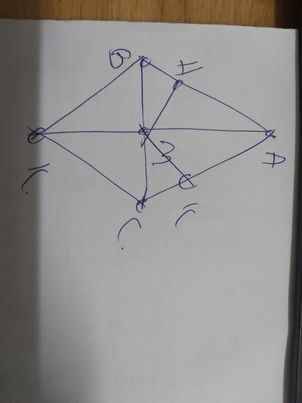
| GT | ΔABC cân tại A M là trung điểm của BC MK=MA MH\(\perp\)AB; MK\(\perp\)AC H\(\in\)AB; K\(\in\)AC |
| KL | b: ΔABM=ΔACM c: ΔABM=ΔKCM d: AB//CK e: MH=MK |
b: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
c: Xét ΔMAB và ΔMKC có
MA=MK
\(\widehat{AMB}=\widehat{KMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMKC
d: Ta có: ΔMAB=ΔMKC
=>\(\widehat{MAB}=\widehat{MKC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//KC
e: ΔAMB=ΔAMC
=>\(\widehat{MAB}=\widehat{MAC}\)
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
=>MH=MK
=>ΔMHK cân tại M
\(a,\left\{{}\begin{matrix}MB=MC\\AB=AC\\AM\text{ chung}\end{matrix}\right.\Rightarrow\Delta ABM=\Delta ACM\left(c.c.c\right)\\ b,\left\{{}\begin{matrix}AM=ME\\BM=MB\\\widehat{AMB}=\widehat{EMC}\left(đđ\right)\end{matrix}\right.\Rightarrow\Delta AMB=\Delta EMC\left(c.g.c\right)\\ \Rightarrow\widehat{ABC}=\widehat{BME}\\ \text{Mà 2 góc này ở vị trí slt nên }AB\text{//}EC\\ c,\Delta AMB=\Delta AMC\\ \Rightarrow\widehat{AMB}=\widehat{AMC}\widehat{AMC}\\ \text{Mà }\widehat{AMC}+\widehat{AMB}=180^0\\ \Rightarrow\widehat{AMC}=\widehat{AMB}=90^0\\ \Rightarrow AM\bot BC\)