Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b)vì AE=AF=>A cách đều AE và AF=>HA nằm trên tia phân giác góc MHN
còn câu c) mình hk biết âu

a, Ta thấy AB là là trung trực của EH nên AE= AH
tương trự AC là trung trực của HF nên AF=AH
Xét tam giác AEF có AF=AE
vậy tram giác AEF cân tại A
b, Ta thấy BA là trung trực EH nên AEH=AHE
IEH=IHE
suy ra AEI =AHI
Tương tự ta suy ra được được AHK=AFK
mà AFK=AEI nên AHI=AHK
vậy HA là tia phân giác của IHK

Bé tự vẽ hình nhé!
a. Vì AB là trung trực của EH nên ta có: AE = AH (1)
Vì AC là trung trực của HF nên ta có: AH = AF (2)
Từ (1) và (2) ta suy ra AE = AF.
b. Vì M thuộc AB nên MB là phân giác \(\widehat{EMH}\)
=> MB là phân giác ngoài góc M của tam giác MNH
Vì N thuộc AC nên NC là phân giác \(\widehat{FNH}\)
=> NC là phân giác ngoài góc N của tam giác \(MNH\)
Do MB và NC cắt nhau tại A nên HA là phân giác trong góc H của tam giác HMN hay HA là phân giác của \(\widehat{MHN}\)
c. Ta có AH \(\perp\) BC (gt) mà HM là phân giác \(\widehat{MHN}\)
=> HB là phân giác ngoài góc H của tam giác HMN
MB là phân giác ngoài góc M của tam giác HMN (cmt)
=> NB là phân giác trong góc N của tam giác HMN
=> NB \(\perp\) AC (2 đường phân giác của hai góc kề bù thì vuông góc với nhau)
=> BN // HF (cùng vuông góc với AC)
CMTT được CM // HE

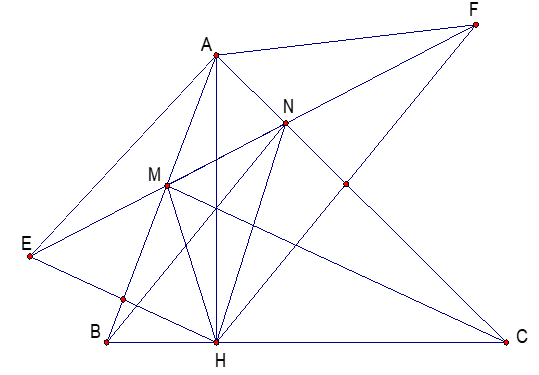
a. Vì AB là trung trực của EH nên ta có: AE = AH (1)
Vì AC là trung trực của HF nên ta có: AH = AF (2
Từ (1) và (2) suy ra: AE = AF
b.

c.


a. Vì AB là trung trực của EH nên ta có: AE = AH (1)
Vì AC là trung trực của HF nên ta có: AH = AF (2)
Từ (1) và (2) suy ra: AE = AF
b.
. 
c.


a) Ta có: AC là đường trung trực của HF(gt)
⇔A nằm trên đường trung trực của HF
⇔AH=AF(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: AB là đường trung trực của HE(gt)
⇔A nằm trên đường trung trực của HE
⇔AH=AE(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AF=AE(Đpcm)