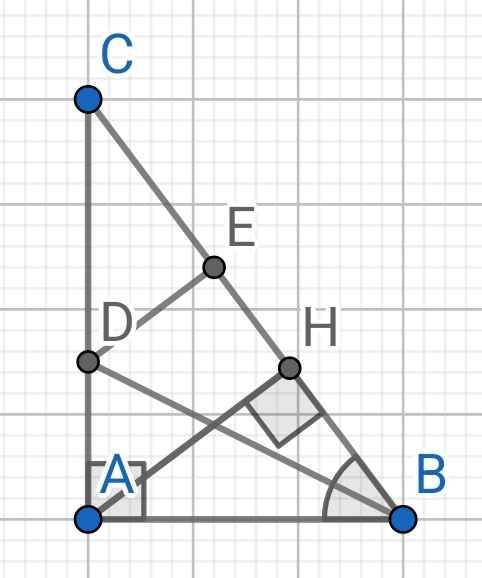
Cho tam giác ABC vuông tại A. Tia phân giác của góc ABC là BD, DE vuông góc BC tại E. Tia ED cắt tia BA tại F . Chứng minh
a) Tam giác ABD = Tam giác EBD
b) AF=EC
Tam giác BFC cân
c) AE//FC
d) BD vuông góc FC
GIÚP EM VỚI SẮP NỘP BÀI RỒI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 5 2021
a). Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
BD là cạnh chung
Góc ABD = góc EBD (đường phân giác BD)
=> tam giác ABD=tam giác EBD (cạnh huyền-góc nhọn)
13 tháng 5 2021
a) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(cạnh huyền-góc nhọn)
24 tháng 8 2023
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>DA=DE
Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
=>ΔDAF=ΔDEC
=>DF=DC
=>ΔDFC cân tại D
c: Xét ΔBFC có
FE,CAlà đường cao
FE cắt CA tại D
=>D là trực tâm
=>BD vuông góc CF tại H
=>DH vuông góc CF tại H
mà ΔDFC cân tại D
nên H là trung điểm của FC
Xét ΔKFC có
CD là trung tuyến
CI=2/3CD
Do đó: I là trọng tâm
mà H là trung điểm của CF
nên K,I,H thẳng hàng
30 tháng 4 2023
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: Xét ΔDAN vuông tại A và ΔDEC vuông tại E có
DA=DE
góc ADN=góc EDC
=>ΔDAN=ΔDEC
=>AN=EC
c: BA+AN=BN
BE+EC=BC
mà BA=BE; AN=EC
nên BN=BC
=>ΔNBC cân tại B
mà BD là phân giác
nên BD vuôg góc NC
16 tháng 4 2023
a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>góc BED=90 độ
=>DE vuông góc CB
c: BA=BE
DA=DE
=>BD là trung trực của AE
d: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
AF=EC
=>ΔDAF=ΔDEC
=>góc ADF=góc EDC
=>góc ADF+góc ADE=180 độ
=>F,D,E thẳng hàng
KV
10 tháng 12 2023
Sửa đề:
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BA = BE. BD là tia phân giác của góc ABC, AH vuông góc với BC. Chứng minh:
a, Tam giác ABD = tam giác EBD
b, AH // DE
Giải
a) Do BD là tia phân giác của ∠ABC (gt)
⇒ ∠ABD = ∠CBD
⇒ ∠ABD = ∠EBD
Xét ∆ABD và ∆EBD có:
BD là cạnh chung
∠ABD = ∠EBD (cmt)
BA = BE (gt)
⇒ ∆ABD = ∆EBD (c-g-c)
b) Do ∆ABD = ∆EBD (cmt)
⇒ ∠BAD = ∠BED (hai góc tương ứng)
⇒ ∠BED = 90⁰
⇒ DE ⊥ BC
Mà AH ⊥ BC (gt)
⇒ AH // DE
10 tháng 12 2023
Để chứng minh a, ta cần chứng minh hai tam giác ABD và EBD có cạnh và góc tương ứng bằng nhau.
Vì tam giác ABC vuông tại A, nên ta có góc ABC = 90 độ. Vì BD là tia phân giác của góc ABC, nên ta có góc ABD = góc DBC.
Vì BA = BE, và góc ABD = góc DBC, nên ta có hai cạnh và góc tương ứng bằng nhau, theo nguyên tắc cạnh-góc-cạnh (SAS), ta có tam giác ABD = tam giác EBD.
Để chứng minh b, ta cần chứng minh hai đường thẳng AH và DE là song song.
Vì tam giác ABC vuông tại A, nên ta có góc ABC = 90 độ. Vì BD là tia phân giác của góc ABC, nên ta có góc ABD = góc DBC.
Vì tam giác ABD = tam giác EBD (đã chứng minh ở câu a), nên ta có góc ADB = góc EDB.
Vì góc ADB = góc EDB và góc ABD = góc DBC, nên theo nguyên tắc góc tương đương, ta có AH // DE.
Vậy, ta đã chứng minh được cả hai phần a và b.
a) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(cạnh huyền-góc nhọn)
b) Ta có: ΔABD=ΔEBD(cmt)
nên AD=ED(hai cạnh tương ứng)
Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE(cmt)
\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔADF=ΔEDC(cạnh góc vuông-góc nhọn kề)
Suy ra: AF=EC(hai cạnh tương ứng)
Ta có: ΔADB=ΔEDB(cmt)
nên BA=BE(hai cạnh tương ứng)
Ta có: BA+AF=BF(A nằm giữa B và F)
BE+EC=BC(E nằm giữa B và C)
mà BA=BE(cmt)
và AF=EC(cmt)
nên BF=BC
Xét ΔBFC có BF=BC(cmt)
nên ΔBFC cân tại B(Định nghĩa tam giác cân)
bạn ơi , mình chỗ góc BC là cạnh Bc chứ nhỉ