giúp mình bài của phần nhóm 1 với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
26 tháng 2 2021
Trong mỗi chúng ta chắc hẳn ai cũng biết đến những nhóm nhạc Hàn Quốc nởi tiếng như MAMAMOO, BTS,Blackpink, Red velvet,..... Nhưng trong số đó em thích nhất là nhóm nhạc Blackpink, đặc biệt là thành viên Jisoo.
Jisoo lớn tuổi nhất nên là chị cả của nhóm nhạc Kpop Blackpink. Họ tên thật của cô là Kim Ji-soo, sinh ngày 3 tháng 1 năm 1995 tại phường Sanbon-dong, thành phố Gunpo, tỉnh Gyeonggi, Hàn Quốc. Cô được trở thành thực tập sinh chính thức của công ty YG Entertainment vào tháng 7 năm 2011 và được đào tạo làm thực tập sinh 5 năm. Jisoo đảm nhận vị trí hát phụ và là người mẫu chính trong nhóm.
Jisoo có làn da trắng hồng rất đẹp. Thân hình mảnh mai, cân đối. Jisoo có vóc người nhỏ nhắn, khuôn mặt luôn tươi cười rạng rỡ khiến bất kỳ trái tim nào cũng phải “rung động”mỗi khi nhìn ngắm. Đôi mắt sáng trong luôn ánh lên vẻ dễ thương nhưng không kém phần quyến rũ. Đôi môi hình trái tim đặc biệt của cô luôn phù hợp với mọi màu son dù là đẹp hay là xấu. Mái tóc dài mượt mà, nhuộm màu vào thì lại càng thêm phần hấp dẫn. Đôi chân thon gọn và dài thẳng tắp.
Cô sở hữu ngoại hình và nhan sắc đẹp trong veo như thiên thần xuống trần gian, ngay từ khi mới ra mắt, Jisoo đã nhanh chóng thu hút được nhiều sự chú ý của người hâm mộ. Cô nàng luôn nhận được rất nhiều lời khen ngợi và được xếp vào hàng những “nữ thần” mới của làng giải trí Hàn Quốc.
Jisoo ở đời thường và trên sân khấu là hai người khác nhau "một trời một vực". Cô nàng mặc dù luôn vui vẻ, tinh nghịch ở phía sau hậu trường là thế nhưng chỉ cần bước lên sân khấu, Jisoo lại vô cùng nghiêm túc và chuyên nghiệp trong từng tiết mục biểu diễn. Từ việc “cháy” hết mình cùng vũ đạo mạnh mẽ cho đến cái nhìn đầy cuốn hút, cô đều cố gắng thể hiện dể phần trình diễn luôn trọn vẹn.
Jisoo sở hữu tính cách hoạt bát, vui nhộn. Bên cạnh đó, Jisoo cũng là cây hút fan của nhóm.“Đẹp người lại còn đẹp cả nết” chính là câu nói rõ ràng nhất để miêu tả về cô nàng Jisoo. Ngay từ khi còn đi học, nữ ca sĩ nhà YG đã được nhận xét là một cô học trò được luôn được thầy cô bạn bè yêu mến vì tính cách hòa đồng, thân thiện của mình.
Có thể nói, Jisoo là thành viên được đánh giá cao nhất Blackpink. Em đã luôn có ước mơ trở thành một nàng ca sĩ giỏi giang giống như Jisoo. Vậy nên em sẽ cố gắng học tập thật tốt để trở thành một người ca sĩ thành đạt như cô.
T
26 tháng 2 2021
“You’re the cause of my euphoria”. Đó là câu hát em thích nhất trong “Euphoria” của Jungkook (thành viên nhỏ tuổi nhất của nhóm nhạc Hàn Quốc – BTS). Và hình ảnh Jungkook biểu diễn “Euphoria” trên sân khấu tại sân vận động Wembley đã để lại trong em nhiều ấn tượng khó phai mờ. Đó là một màn biểu diễn rất tuyệt vời và xúc động của một chàng ca sĩ trẻ tuổi giàu đam mê, nhiệt huyết, muốn cháy hết mình trên sân khấu và đem tới cho fan hâm mộ những giây phút thoải mái nhất khi tham gia concert của nhóm. Em thực sự thích màn biểu diễn đó.
Khi ánh đèn sân khấu được thắp lên, tiếng hò reo của fan hâm mộ vang thật lớn trong sân vận động rộng mênh mông, Jungkook tự tin bước ra sân khấu cùng với dàn vũ công đằng sau. “You’re the cause of my euphoria” – câu hát Jungkook cất lên bằng một chất giọng rất thanh, rất mảnh nhưng lại cao vút và đầy nội lực. Giọng hát không cần quá nhiều về kỹ thuật thanh nhạc nhưng lạ tràn đầy cảm xúc động tới nơi sâu thẳm nhất trong trái tim người hàng nghìn người hâm mộ trong sân vận động. Đi kèm theo hát, mà biểu diễn còn có vũ đạo. Những bước nhảy, xoay người, tay và chân của Jungkook đều kết hợp với nhau vô cùng nhịp nhàng và bắt mắt. Vũ đạo vừa ôn vừa nhu, có chút mạnh mẽ khỏe khoắn nhưng đồng thời cũng rất nhẹ nhàng và uyển chuyển. Đặc biệt, tới đoạn cao trào, Jungkookie với thiết bị dây đai vô cùng chắc chắn đã bay lên không trung bởi cậu ấy muốn được nhìn thấy nhiều fan hâm mộ hơn trong sân vận động rộng lớn này, muốn gần ARMY hơn (tên fandom của BTS). Jungkook vừa hát vừa bay trên không trung vừa hát như một chú chim đang tự do sải cánh và cất tiếng hát ngọt ngào trên bầu trời xanh thẳm. Jungkook mang âm nhạc và tiếng nói của mình tới nhiều người trên khắp thế giới hơn. Và ngay cả khi vừa bay vừa hát thì giọng của Jungkook vẫn rất vững và đúng nhịp.
Em xem hết màn biểu diễn mà phải vừa nín thở vừa xem. Màn biểu diễn của Jungkook kết thúc nhưng vẫn để lại trong em những dư âm dư ba tuyệt vời. Một màn biểu diễn xuất sắc!
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
1.
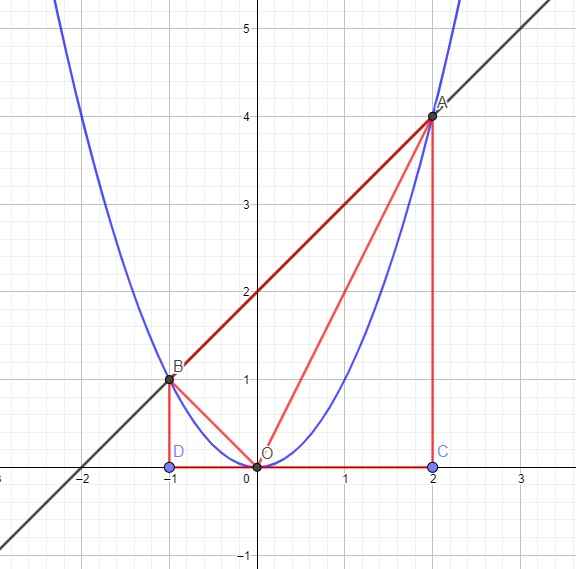
Dễ dàng tìm được tọa độ 2 giao điểm, do vai trò của A, B như nhau, giả sử \(A\left(2;4\right)\) và \(B\left(-1;1\right)\)
Gọi C và D lần lượt là 2 điểm trên trục Ox có cùng hoành độ với A và B, hay \(C\left(2;0\right)\) và \(D\left(-1;0\right)\)
Khi đó ta có ABDC là hình thang vuông tại D và C, các tam giác OBD vuông tại D và tam giác OAC vuông tại C
Độ dài các cạnh: \(BD=\left|y_B\right|=1\) ; \(AC=\left|y_A\right|=4\)
\(OD=\left|x_D\right|=1\) ; \(OC=\left|x_C\right|=2\) ; \(CD=\left|x_C-x_D\right|=3\)
Ta có:
\(S_{OAB}=S_{ABDC}-\left(S_{OBD}+S_{OAC}\right)\)
\(=\dfrac{1}{2}CD.\left(AC+BD\right)-\left(\dfrac{1}{2}BD.OD+\dfrac{1}{2}AC.OC\right)\)
\(=\dfrac{1}{2}.3.\left(4+1\right)-\left(\dfrac{1}{2}.1.1+\dfrac{1}{2}.4.2\right)=3\)
27 tháng 9 2021
1b) \(C=\sqrt{81a}-\sqrt{144a}+\sqrt{36a}\left(a\ge0\right)=8\sqrt{a}-12\sqrt{a}+6\sqrt{a}=2\sqrt{a}\)
Bài 2:
a),b) \(P=\left(\dfrac{1}{1-\sqrt{a}}-\dfrac{1}{1+\sqrt{a}}\right)\left(\dfrac{1}{\sqrt{a}}+1\right)\left(đk:x>0,x\ne1\right)\)
\(=\dfrac{1+\sqrt{a}-1+\sqrt{a}}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}.\dfrac{\sqrt{a}+1}{\sqrt{a}}=\dfrac{2\sqrt{a}}{1-\sqrt{a}}.\dfrac{1}{\sqrt{a}}=\dfrac{2}{1-\sqrt{a}}\)
c) \(P=\dfrac{2}{1-\sqrt{a}}=\dfrac{2}{1-\sqrt{4}}=\dfrac{2}{1-2}=-2\)
d) \(P=\dfrac{2}{1-\sqrt{a}}=9\)
\(\Rightarrow-9\sqrt{a}+9=2\Rightarrow\sqrt{a}=\dfrac{7}{9}\Rightarrow a=\dfrac{49}{81}\left(tm\right)\)
TA
0
DN
4
C
10 tháng 3 2018
\(\frac{1}{3}\times X=\frac{1}{6}\)
\(X=\frac{1}{6}\div\frac{1}{3}\)
\(X=\frac{1}{2}\)
TM
6 tháng 4 2023
Bài III.2b.
Phương trình hoành độ giao điểm của \(\left(P\right)\) và \(\left(d\right)\) : \(x^2=\left(m+1\right)x-m-4\)
hay : \(x^2-\left(m+1\right)x+m+4=0\left(I\right)\)
\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm nên phương trình \(\left(I\right)\) sẽ có hai nghiệm phân biệt. Do đó, phương trình \(\left(I\right)\) phải có :
\(\Delta=b^2-4ac=\left[-\left(m+1\right)\right]^2-4.1.\left(m+4\right)\)
\(=m^2+2m+1-4m-16\)
\(=m^2-2m-15>0\).
\(\Rightarrow m< -3\) hoặc \(m>5\).
Theo đề bài : \(\sqrt{x_1}+\sqrt{x_2}=2\sqrt{3}\)
\(\Rightarrow\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=\left(2\sqrt{3}\right)^2=12\)
\(\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2}=12\left(II\right)\)
Do phương trình \(\left(I\right)\) có hai nghiệm khi \(m< -3\) hoặc \(m>5\) nên theo định lí Vi-ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(m+1\right)}{1}=m+1\\x_1x_2=\dfrac{c}{a}=\dfrac{m+4}{1}=m+4\end{matrix}\right.\).
Thay vào \(\left(II\right)\) ta được : \(m+1+2\sqrt{m+4}=12\)
Đặt \(t=\sqrt{m+4}\left(t\ge0\right)\), viết lại phương trình trên thành : \(t^2-3+2t=12\)
\(\Leftrightarrow t^2+2t-15=0\left(III\right)\).
Phương trình \(\left(III\right)\) có : \(\Delta'=b'^2-ac=1^2-1.\left(-15\right)=16>0\).
Suy ra, \(\left(III\right)\) có hai nghiệm phân biệt :
\(\left\{{}\begin{matrix}t_1=\dfrac{-b'+\sqrt{\Delta'}}{a}=\dfrac{-1+\sqrt{16}}{1}=3\left(t/m\right)\\t_2=\dfrac{-b'-\sqrt{\Delta'}}{a}=\dfrac{-1-\sqrt{16}}{1}=-5\left(ktm\right)\end{matrix}\right.\)
Suy ra được : \(\sqrt{m+4}=3\Rightarrow m=5\left(ktm\right)\).
Vậy : Không có giá trị m thỏa mãn đề bài.
TM
6 tháng 4 2023
Bài IV.b.
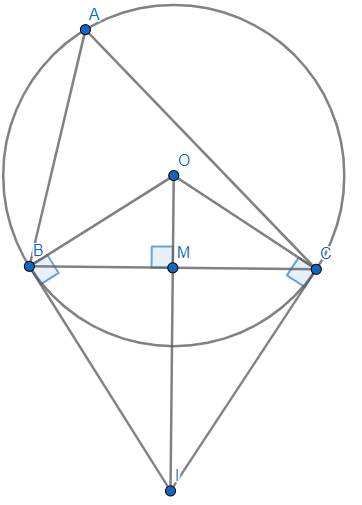
Chứng minh : Ta có : \(OB=OC=R\) nên \(O\) nằm trên đường trung trực \(d\) của \(BC\).
Theo tính chất hai tiếp tuyến cắt nhau thì \(IB=IC\), suy ra \(I\in d\).
Suy ra được \(OI\) là một phần của đường trung trực \(d\) của \(BC\) \(\Rightarrow OI\perp BC\) tại \(M\) và \(MB=MC\).
Xét \(\Delta OBI\) vuông tại \(B\) có : \(MB^2=OM.OI\).
Lại có : \(BC=MB+MC=2MB\)
\(\Rightarrow BC^2=4MB^2=4OM.OI\left(đpcm\right).\)
Tính diện tích hình quạt tròn
Ta có : \(\hat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\Rightarrow sđ\stackrel\frown{BC}=2.\hat{BAC}=2.70^o=140^o\) (góc nội tiếp).
\(\Rightarrow S=\dfrac{\pi R^2n}{360}=\dfrac{\pi R^2.140^o}{360}=\dfrac{7}{18}\pi R^2\left(đvdt\right)\)
4 tháng 8 2023
Dàn ý:
1. Mở đoạn: Khẳng định ý nghĩa quan trọng của thái độ sống tích cực
2. Thân đoạn:
- Thái độ sống tích cực: việc luôn tìm cách suy nghĩ và cảm nhận thế giới một cách tích cực qua đó tìm thấy niềm vui và ý nghĩa trong cuộc sống.
- Ý nghĩa của thái độ sống tích cực:
+ Cá nhân:
- Tạo động lực mạnh mẽ tiến lên phía trước
- Học được cách hài lòng với những gi mình đang có
- Tìm thấy lối thoát trong những hoàn cảnh khó khăn nhất
Dẫn chứng: Nhà văn Andecsen ( hoàn cảnh sinh ra bất hạnh nhưng ông luôn giữ được thái độ sống tích cực => ông đã trở thành nhà văn nổi tiếng thắp sáng ước mơ cho hàng nghìn đứa trẻ trên thế giới )
+ Cộng đồng:
- Lan tỏa những giá trị tốt đẹp trong xã hội, nâng đỡ những người hoàn cảnh khó khăn hơn
- Bài học nhận thức: Chúng ta cần sống với thái độ tích cực nhưng cũng phải nhìn nhận thực tế để sửa đổi.
=> Liên hệ bản thân
NA
0