\(\left(x^2+1-x^3\right)^8\) xác định hệ số x8 trong khai triển
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 9 2021
Xét khai triển : (x + 1)n
Tk+1 = \(C_n^k\). xk . 110 - k = \(C_n^k\) . xk.
+) Cụ thể với khai triển (x + 1)10. Số hạng chứa x8 ứng với k = 8
Số hạng x8 trong khai triển này là \(C_{10}^8\) . x8 = 45x8
+) Cụ thể với khai triển (x + 1)11. Số hạng chứa x8 ứng với k = 8
Số hạng x8 trong khai triển này là \(C_{11}^8\) . x8 = 165x8
+) Cụ thể với khai triển (x + 1)12. Số hạng chứa x8 ứng với k = 8
Số hạng x8 trong khai triển này là \(C_{12}^8\) . x8 = 495x8
Vậy hệ số của x8 trong khai triển của đa thức trên là : 165 + 495 + 45 = 705
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
+) Ta có:
\(\begin{array}{l}{\left( {3x + 2} \right)^5} = {\left( {3x} \right)^5} + 5.{\left( {3x} \right)^4}2 + 10.{\left( {3x} \right)^3}{2^2} + 10{\left( {3x} \right)^2}{.2^3} + 5.\left( {3x} \right){.2^4} + {2^5}\\ = 243{x^5} + 810{x^4} + 1080{x^3} + 720{x^2} + 240x + 32\end{array}\)
+) Hệ số của \({x^4}\) trong khai triển trên là: \({a_4} = 810\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 11 2019
\(\left(x^{-4}+x^{\frac{5}{2}}\right)^{12}\) có SHTQ: \(C_{12}^kx^{-4k}.x^{\frac{5}{2}\left(12-k\right)}=C^k_{12}x^{30-\frac{13}{2}k}\)
Số hạng chứa \(x^8\Rightarrow30-\frac{13}{2}k=8\Rightarrow\) ko có k nguyên thỏa mãn
Vậy trong khai triển trên ko có số hạng chứa \(x^8\)
b/ \(\left(1-x^2+x^4\right)^{16}\)
\(\left\{{}\begin{matrix}k_0+k_2+k_4=16\\2k_2+4k_4=16\end{matrix}\right.\)
\(\Rightarrow\left(k_0;k_2;k_4\right)=\left(8;8;0\right);\left(9;6;1\right);\left(10;4;2\right);\left(11;2;3\right);\left(12;0;4\right)\)
Hệ số của số hạng chứa \(x^{16}\):
\(\frac{16!}{8!.8!}+\frac{16!}{9!.6!}+\frac{16!}{10!.4!.2!}+\frac{16!}{11!.2!.3!}+\frac{16!}{12!.4!}=...\)
c/ SHTQ của khai triển \(\left(1-2x\right)^5\) là \(C_5^k\left(-2\right)^kx^k\)
Số hạng chứa \(x^4\) có hệ số: \(C_5^4.\left(-2\right)^4\)
SHTQ của khai triển \(\left(1+3x\right)^{10}\) là: \(C_{10}^k3^kx^k\)
Số hạng chứa \(x^3\) có hệ số \(C_{10}^33^3\)
\(\Rightarrow\) Hệ số của số hạng chứa \(x^5\) là: \(C_5^4\left(-2\right)^4+C_{10}^3.3^3\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 11 2019
Làm xong rồi nhấn gửi thì lỗi, làm lại từ đầu nên chỉ làm 2 câu thôi, 2 câu sau bạn tự làm tương tự:
a/ \(\sum\limits^8_{k=0}C_8^kx^{2k}\left(1-x\right)^k=\sum\limits^8_{k=0}\sum\limits^k_{i=0}C_8^kC_k^i\left(-1\right)^ix^{2k+i}\)
Số hạng chứa \(x^8\) có:
\(\left\{{}\begin{matrix}2k+i=8\\0\le i\le k\le8\\i;k\in N\end{matrix}\right.\) \(\Rightarrow\left(i;k\right)=\left(0;4\right);\left(2;3\right)\)
Hệ số: \(C_8^4C_4^0.\left(-1\right)^0+C_8^3C_3^2.\left(-1\right)^2\)
b/ \(1+x+x^2+x^3=\left(1+x\right)\left(1+x^2\right)\)
\(\Rightarrow\left(1+x+x^2+x^3\right)^{10}=\left(1+x\right)^{10}\left(1+x^2\right)^{10}\)
\(=\sum\limits^{10}_{k=0}C_{10}^kx^k\sum\limits^{10}_{i=0}C_{10}^ix^{2i}=\sum\limits^{10}_{k=0}\sum\limits^{10}_{i=0}C_{10}^kC_{10}^ix^{2i+k}\)
Số hạng chứa \(x^5\) có:
\(\left\{{}\begin{matrix}2i+k=5\\0\le k\le10\\0\le i\le10\\i;k\in N\end{matrix}\right.\) \(\Rightarrow\left(i;k\right)=\left(0;5\right);\left(1;3\right);\left(2;1\right)\)
Hệ số: \(C_{10}^0C_{10}^5+C_{10}^1C_{10}^3+C_{10}^2C_{10}^1\)
CM
15 tháng 9 2017
Lời giải.
Cách 1:
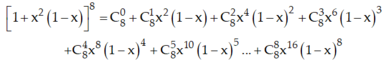
Trong khai triển trên ta thấy bậc của x trong 3 số hạng đầu nhỏ hơn 8, bậc của x trong 4 số hạng cuối lớn hơn 8.
Do đó x8 chỉ có trong số hạng thứ tư, thứ năm với hệ số tương ứng là:
.
Vậy hệ số cuả x8 trong khai triển đa thức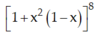 
là:
Cách 2: Ta có:
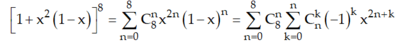
với 0 ≤ k ≤ n ≤ 8.
Số hạng chứa x8 ứng với 2n + k = 8 ⇒ k = 8 -2n là một số chẵn.
Thử trực tiếp ta được k = 0, n =4 và k = 2, n = 3.
Vậy hệ số của x8 là 
Chọn C.
\(\left(x^2+1-x^3\right)^8=\sum\limits^8_{k=0}C^k_8.\left(x^2-x^3\right)^k\)
\(=\sum\limits^8_{k=0}C^k_8\sum\limits^k_{i=0}C^i_k.\left(x^2\right)^{k-i}\left(x^3\right)^i\)
\(=\sum\limits^8_{k=0}\sum\limits^k_{i=0}C^k_8C^i_k.x^{2k+i}\)
\(\Rightarrow2k+i=8\)
Ta có: \(\left\{{}\begin{matrix}2k+i=8\\i\in N\\k\in N\\0\le i\le k\le8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}i=2\\k=3\end{matrix}\right.\)
\(\Rightarrow\) Hệ số của \(x^8\) trong khai triển là \(C^3_8C^2_3=168\).