ai là CTV xóa dùm em hết câu hỏi trong tài khoản này với ạ :((( em cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,B=\dfrac{2+3}{2.2+3}=\dfrac{5}{7}\\ b,A=\dfrac{\sqrt{x}+15-x-3\sqrt{x}+2x-\sqrt{x}-15}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ A=\dfrac{x-3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+3}\\ c,P=AB=\dfrac{\sqrt{x}}{2\sqrt{x}-3}< \dfrac{1}{2}\Leftrightarrow\dfrac{\sqrt{x}}{2\sqrt{x}-3}-\dfrac{1}{2}< 0\\ \Leftrightarrow\dfrac{2\sqrt{x}-2\sqrt{x}+3}{2\left(2\sqrt{x}-3\right)}< 0\Leftrightarrow\dfrac{3}{2\left(2\sqrt{x}-3\right)}< 0\\ \Leftrightarrow2\sqrt{x}-3< 0\left(3>0\right)\\ \Leftrightarrow\sqrt{x}< \dfrac{3}{2}\Leftrightarrow0< x< \dfrac{9}{4}\)




3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
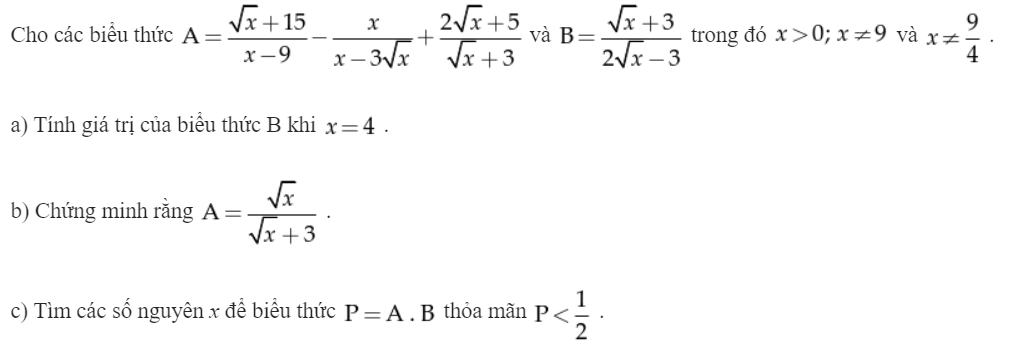




ủa sao lại xóa:)??
Mà CTV ko rảnh đâu nên đừng nhờ nha!
bn tự xóa đc