Tìm số nguyên x
2x+\(|x|\)=3x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
NM
0
PT
1
CM
28 tháng 12 2018
Đáp án: A.
Hướng dẫn: Ta có B, C và D. Chỉ kiểm tra D đúng, còn B và C sai khác với D hằng số -1, 1.
PT
1
CM
31 tháng 8 2017
Chọn A.
Điều kiện: x > 1
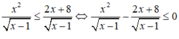
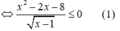
Vì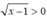 
với ∀x > 1 nên bất phương trình (1) tương đường với x2 - 2x - 8 ≤ 0 ⇔ -2 ≤ x ≤ 4.
Kết hợp với điều kiện x > 1 suy ra 1 ≤ x ≤ 4 ⇒ x ∈ {2;3;4}
Vậy bất phương trình có ba nghiệm nguyên.
2x+/x/=3x ( / / là giá trị tuyệt đối nha bạn )
/x/=3x-2x
/x/=x
Do giá trị tuyệt đối của bất kì số nguyên nào đều không bao giờ là số nguyên âm nên x phải lớn hơn -1
\(\Rightarrow x\in N\)
`2x+|x|=3x`
`=>|x|=3x-2x`
`=>|x|=x`
Sử dụng tính chất `|A|=|A|<=>A>=0`
`=>x>=0`
Vậy với `x>=0` thì `2x+|x|=3x`