Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
(3,0 điểm)
Tóm tắt: (0,5 điểm)
s 1 = 300m; t 1 = 2 phút = 120 s
s 2 = 500m; t 2 = 2,5 phút = 150 s
Tính: v tb = ?
Giải
Vận tốc trung bình của người đi xe đạp trên cả hai quãng đường là: (0,5 điểm)
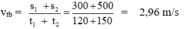(0,5 điểm)
20'=1/3h
10'=1/6h
20s=1/180h
4m/s=14,4km/h
ta có:
quãng đường xe lăn được là:
S3=v3t3=0,08km
vận tốc trung bình của xe là:
\(v_{tb}=\frac{S_1+S_2+S_3}{t_1+t_2+t_3}\approx18\) km/h
Tóm tắt
$s_1=130m$
$t_1=\dfrac{1}{4}$ phút$=15$ giây
$s_1=60m$
$t_2=20$ giây
$v_{tb}=?$
Giải
Vận tốc trung bình của người đi xe đạp trên cả hai quãng đường là:
$v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{130+60}{15+20}=7,2 (m/s)$
Đáp số: $7,2 (m/s)$
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{130+60}{\dfrac{1}{4}.60+20}=...\left(m/s\right)\)
\(\left\{{}\begin{matrix}v'=s':t'=480:\left(2.60\right)=4\left(\dfrac{m}{s}\right)\\v''=s'':t''=60:24=2,5\left(\dfrac{m}{s}\right)\\v_{tb}=\dfrac{s'+s''}{t'+t''}=\dfrac{480+60}{\left(2.60\right)+24}=3,75\left(\dfrac{m}{s}\right)\end{matrix}\right.\)
Vận tốc trung bình xe đi trên quãng đường dốc:
\(v_1=\dfrac{S_1}{t_1}=\dfrac{480}{2\cdot60}=4\)m/s
Vận tốc trung bình trên quãng đường nằm ngang:
\(v_2=\dfrac{S_2}{t_2}=\dfrac{60}{24}=2,5\)m/s
Vận tốc trung bình trên cả quãng đường xe đi:
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{480+60}{2\cdot60+24}=3,75\)m/s
2 phút = 120 giây, 2,5 phút = 150 giây
Vận tốc của người đi xe đạp khi lên dốc la
\(V=\dfrac{s}{t}=120:120=1\left(ms\right)\)
Vận tốc của người đi xe đạp xuống dốc là
\(V=\dfrac{s}{t}=420:150=2,8\left(ms\right)\)
Vận tốc trung bình của người đó trên cả 2 quãng đường là
\(V_{tb}=\dfrac{S+S_1}{t+t_1}=\dfrac{120+420}{120+150}=\dfrac{540}{270}=2\left(ms\right)\)
Đổi 2m/s =7,2 km/h