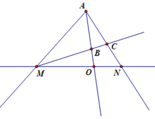
Từ điểm A nằm ngoài (O;R) kẻ hai tiếp tuyến AB và AC (B và C là hai tiếp điểm). Gọi H là trung điểm của BC.
a) Chứng minh O, A, B, C cùng thuộc đường tròn và 3 điểm O, H, A thẳng hàng.
b) Kẻ đường kính CD. AD cắt đường tròn (O)tại điểm thứ hai là E và cắt đường tròn đường kính OA tại I. Chứng minh I là trung điểm của DE.
c) OI cắt BC tại F, Gọi G là giao điểm của OA và FE, OE cắt BC tại M. Chứng minh rằng: GM // DE.





a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp