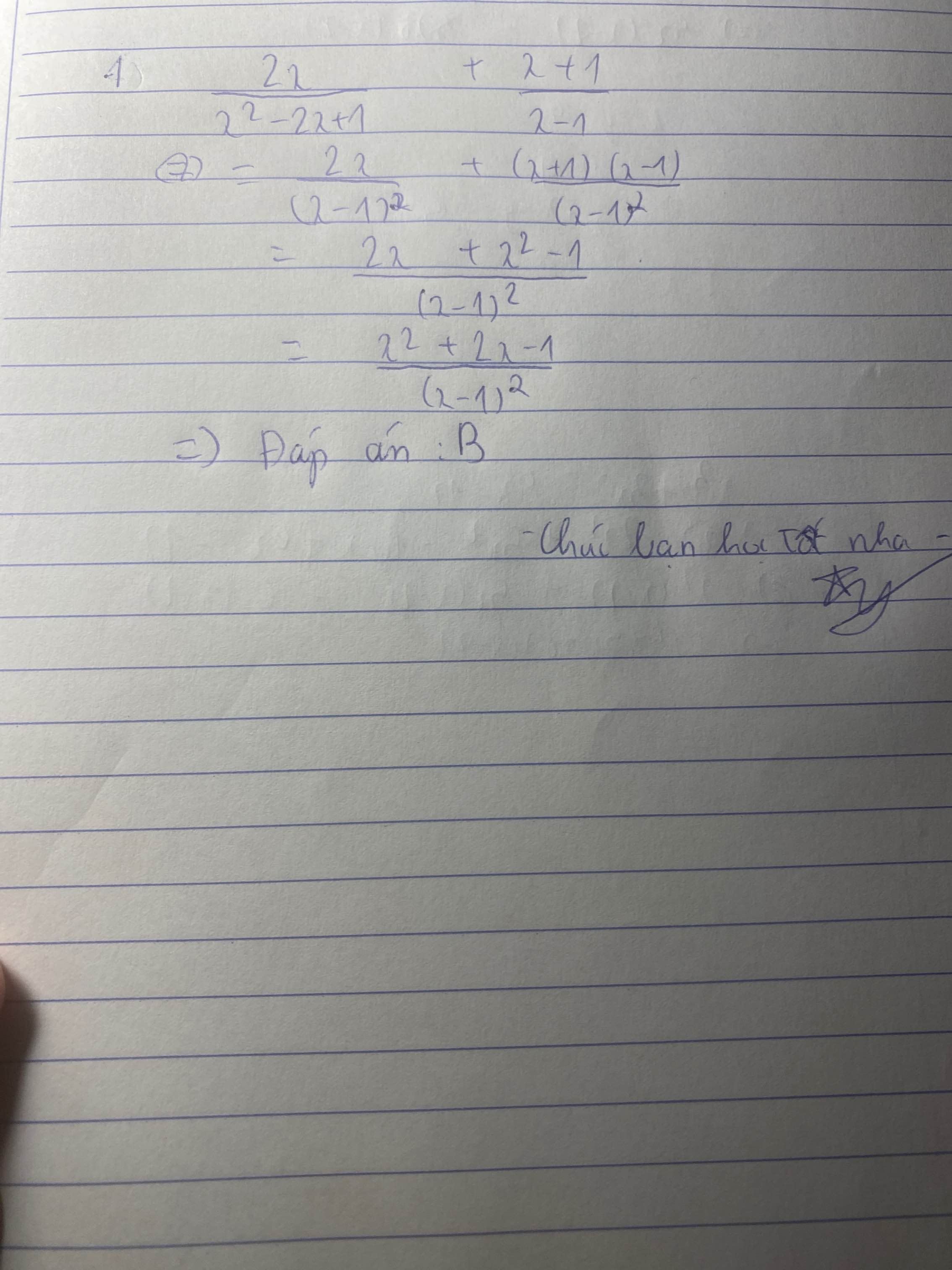1) Thuc hien phep tinh cong 2 phan thuc \(\dfrac{2x}{x^2-2x+1}+\dfrac{x+1}{x-1}\) duoc ket qua la:
A. \(\dfrac{x^2+2x+1}{\left(x-1\right)^2}\) B. \(\dfrac{x^2+2x-1}{\left(x-1\right)^2}\) C. \(\dfrac{x^2-x-1}{\left(x-1\right)^2}\) D. \(\dfrac{x^2-2x-1}{\left(x-1\right)^2}\)