cho hàm số y=-1/2x+3(d)
a)vẽ đồ thị hàm số
b)gọi A,B là giao điểm của d vs các trục tọa độ.Tính diện tích tam giác OAB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: 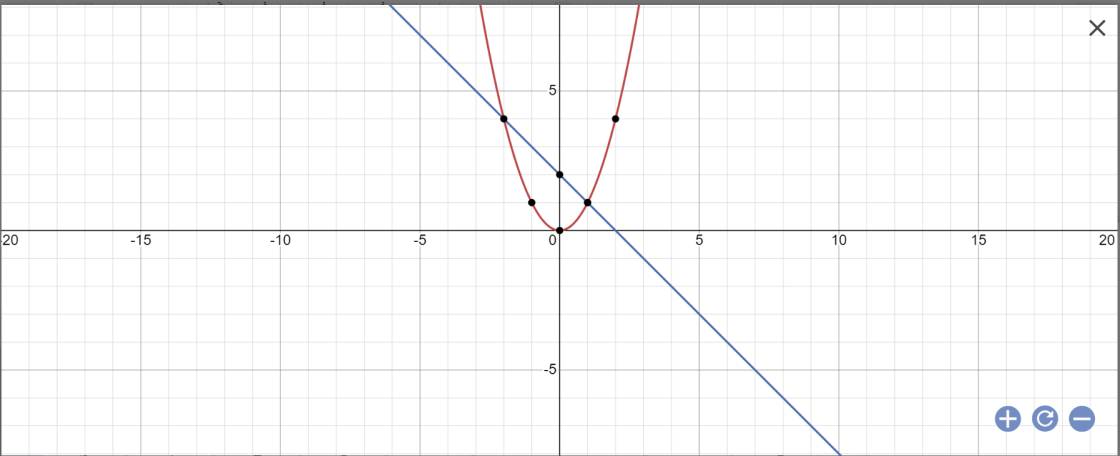
b: PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1

a:
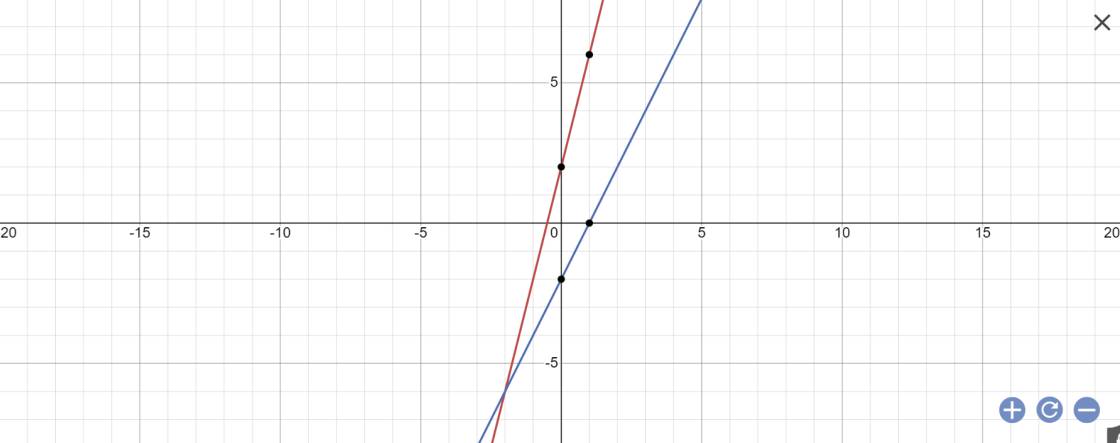
b: phương trình hoành độ giao điểm là:
4x+2=2x-2
=>4x-2x=-2-2
=>2x=-4
=>x=-2
Thay x=-2 vào y=4x+2, ta được:
\(y=4\cdot\left(-2\right)+2=-8+2=-6\)
Vậy: M(-2;-6)
c: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\4x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\4x=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-\dfrac{1}{2}\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\2x-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\2x=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=1\end{matrix}\right.\)
Vậy: B(1;0); A(-1/2;0)
d: M(-2;-6); B(1;0); A(-1/2;0)
\(MA=\sqrt{\left(-\dfrac{1}{2}+2\right)^2+\left(0-6\right)^2}=\dfrac{3\sqrt{17}}{2}\)
\(MB=\sqrt{\left(1+2\right)^2+\left(0+6\right)^2}=3\sqrt{5}\)
\(AB=\sqrt{\left(-\dfrac{1}{2}-1\right)^2+\left(0-0\right)^2}=\dfrac{3}{2}\)
Chu vi tam giác MAB là:
\(C_{MAB}=MA+MB+AB=\dfrac{3}{2}+3\sqrt{5}+\dfrac{3\sqrt{17}}{2}\)
Xét ΔMAB có \(cosAMB=\dfrac{MA^2+MB^2-AB^2}{2\cdot MA\cdot MB}=\dfrac{9}{\sqrt{85}}\)
=>\(sinAMB=\sqrt{1-\left(\dfrac{9}{\sqrt{85}}\right)^2}=\dfrac{2}{\sqrt{85}}\)
Diện tích tam giác MAB là:
\(S_{AMB}=\dfrac{1}{2}\cdot MA\cdot MB\cdot sinAMB=\dfrac{1}{2}\cdot\dfrac{3\sqrt{17}}{2}\cdot3\sqrt{5}\cdot\dfrac{2}{\sqrt{85}}\)
\(=\dfrac{9}{2}\)

b: M thuộc đồ thị vì \(y_M=x_M\)
N thuộc đồ thị vì \(y_N=x_N\)
\(b,\text{PT giao }Ox:y=0\Leftrightarrow x=6\Leftrightarrow A\left(6;0\right)\Leftrightarrow OA=6\\ \text{PT giao }Oy:x=0\Leftrightarrow y=3\Leftrightarrow B\left(0;3\right)\Leftrightarrow OB=3\\ \Leftrightarrow S_{OAB}=\dfrac{1}{2}OA\cdot OB=\dfrac{1}{2}\cdot6\cdot3=9\left(đvdt\right)\)