.Cho tam giác ABC vuông tại A có AC=2AB= 50,8 (cm) Vẽ trung tuyến BM của tam giác ABC và đường cao AH của tam giác ABM. Trên tia đói của tia AH lấy E sao cho AE = BM . Tính chu vi và diện tích của tam giác BCE ? (chính xác đến 0,00001)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 8 2016
Bài 2
gọi E là trung điểm của KB
Vì tam giác CKB có BM=MC ; BE=EK
=>EM//KC
Vì tam giác ENM có AN=AM ; KA//EM
=>EK=KN
Vì KN=KE=EB=>NK=1/2KB
19 tháng 2 2022
a. -Xét △BHE có: BE//AM (gt)
\(\Rightarrow\dfrac{BE}{AM}=\dfrac{BH}{HM}\) (định lí Ta let)
Mà \(\dfrac{BH}{HM}=\dfrac{1}{2}\)(gt)
\(\Rightarrow\dfrac{BE}{AM}=\dfrac{1}{2}\)
-Mà \(AM=\dfrac{1}{2}AC\) (M là trung điểm AC).
\(\Rightarrow\dfrac{BE}{\dfrac{1}{2}AC}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{BE}{AC}=\dfrac{1}{4}\)
b) -Xét △BKE có: BK//AC (gt)
\(\Rightarrow\dfrac{BE}{AC}=\dfrac{BK}{KC}\) (định lí Ta-let)
Mà \(\dfrac{BE}{AC}=\dfrac{1}{4}\left(cmt\right)\)
\(\Rightarrow\dfrac{1}{4}=\dfrac{BK}{KC}\)
\(\Rightarrow KC=4BK\)
Mà \(BK+KC=BC\)
\(\Rightarrow BK+4BK=BC\)
\(\Rightarrow5BK=BC\)
\(\Rightarrow\dfrac{BK}{BC}=\dfrac{1}{5}\)
c) \(\dfrac{S_{ABK}}{S_{ABC}}=\dfrac{BK}{BC}=\dfrac{1}{5}\)
KT
28 tháng 3 2018
a) Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow\)\(BC^2=9^2+12^2=225\)
\(\Leftrightarrow\)\(BC=\sqrt{225}=15\)cm
Diện tích tam giác ABC là:
\(S_{ABC}=\frac{AB.AC}{2}=\frac{9.12}{2}=54\)cm2
b) Xét \(\Delta ABC\)và \(\Delta HBA\) có:
\(\widehat{BAC}=\widehat{BHA}=90^0\)
\(\widehat{ABC}\) chung
suy ra: \(\Delta ABC~\Delta HBA\)
\(\Rightarrow\)\(\frac{AB}{HB}=\frac{BC}{AB}\)
\(\Rightarrow\)\(AB.AB=BH.BC\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
7 tháng 1
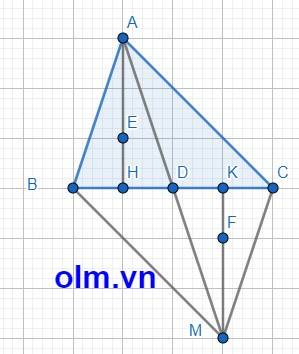
Xét tam giác ACD và tam giác MBD có:
AD = DM (gt)
BD = DC (gt)
\(\widehat{BDM}\) = \(\widehat{ADC}\) (hai góc đối đỉnh)
⇒ \(\Delta\)ACD = \(\Delta\) MBD (c-g-c)
Xét tứ giác ABMC có
AD = DM
BD = DC
⇒ tứ giác ABMC là hình bình hành vì tứ giác có hai đường chéo căt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.
⇒ AC // BM
⇒ \(\widehat{ABM}\) = \(\widehat{MCA}\) (vì tứ giác ABMC là hình bình hành)
K
7 tháng 1
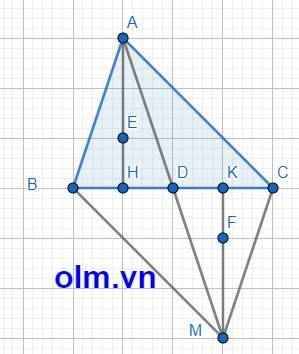
xét tam giác ACD và tam giác MBD có
AD=DM [ gt ]
BD=DC[ gt ]
BDM = ADC hai góc đối đỉnh
suy ra tam giác ACD= tam giác MBD [ c-g-c]
xét tứ giác ABMC có
AD = DM
BD=DC
suy ra tứ giác ABMC là hình bình hành vì tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành
suy ra ABM=MCA vì tứ giác ABMC là hình bình hành .
17 tháng 12 2021
Diện tích tam giác ABM là:
4.3=12(cm2)
Diện tích tam giác ABC là:
4.6=24(cm2)