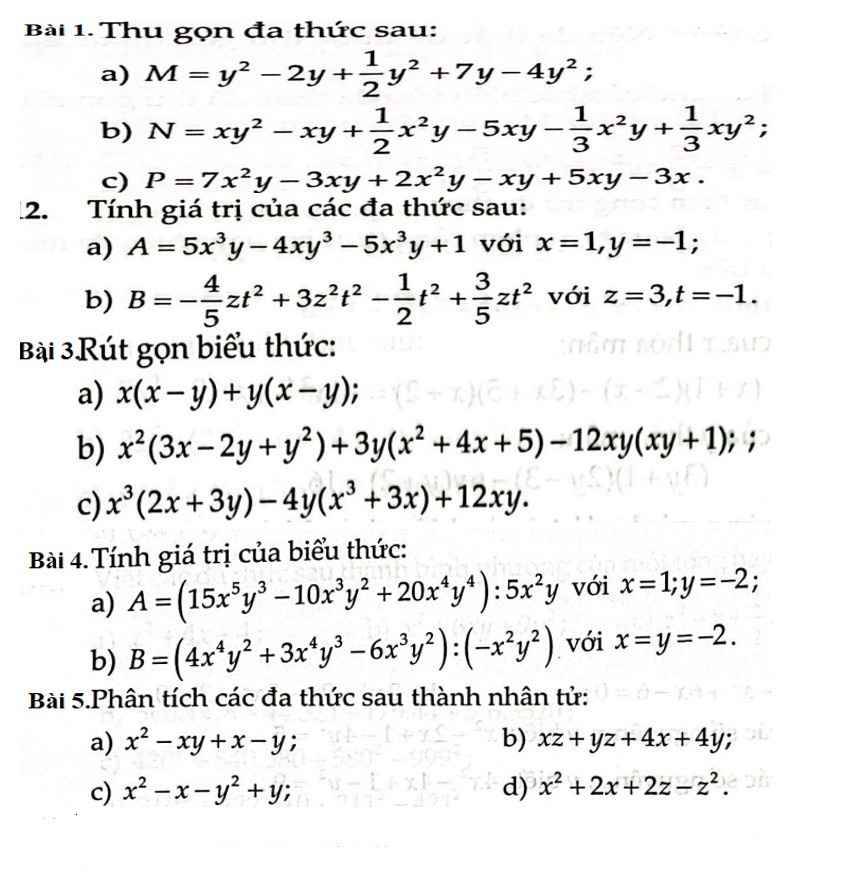Giúp mik bài 1 và bài 3 với ạ ,cám ơn nhìu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
5 tháng 6 2023
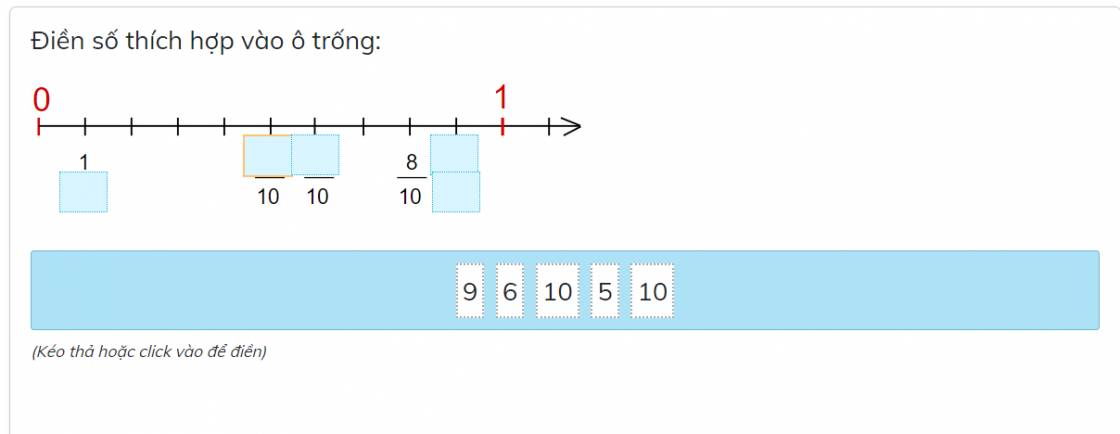
Từ 0 đến 1 được chia thành 10 phần bằng nhau.
Giá trị của mỗi phần là: \(\dfrac{1}{10}\)
Từ lập luận trên ta có:
Số thích hợp để điền vào các ô trống lần lượt là:
10; 5; 6; 9; 10
5 tháng 6 2023
0 ; 1/10 ; 2/10 ; 3/10 ; 4/10 ; 5/10 ; 6/10 ; 7/10 ; 8/10 ; 9/10 ; 1
Chúc bạn học tốt!
DT
3
2 tháng 8 2021
8) \(\dfrac{x+7}{3}+\dfrac{x+5}{4}=\dfrac{x+3}{5}+\dfrac{x+1}{6}\)
\(\Rightarrow\dfrac{x+7}{3}+\dfrac{x+5}{4}-\dfrac{x+3}{5}-\dfrac{x+1}{6}=0\)
\(\Rightarrow\dfrac{x+7}{3}+2+\dfrac{x+5}{4}+2-\dfrac{x+3}{5}-2-\dfrac{x+1}{6}-2=0+2+2-2-2\)
\(\Rightarrow\left(\dfrac{x+7}{3}+2\right)+\left(\dfrac{x+5}{4}+2\right)-\left(\dfrac{x+3}{5}+2\right)-\left(\dfrac{x+1}{6}+2\right)=0\)
\(\Rightarrow\left(\dfrac{x+7}{3}+\dfrac{6}{3}\right)+\left(\dfrac{x+5}{4}+\dfrac{8}{4}\right)-\left(\dfrac{x+3}{5}+\dfrac{10}{5}\right)-\left(\dfrac{x+1}{6}+\dfrac{12}{2}\right)=0\)
\(\Rightarrow\left(x+13\right)\left(\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{5}-\dfrac{1}{6}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+13=0\\\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}=0\end{matrix}\right.\)
\(x+13=0\)
\(\Rightarrow x=-13\)
\(\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}=0\)
\(\dfrac{13}{60}=0\) (vô lí)
Vậy \(x=-13\)
9) Bạn chuyển vế rồi cộng 3 vào từng mỗi số
13 tháng 7 2021
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại B có BH là đường cao ứng với cạnh huyền AC, ta được:
\(BH^2=HA\cdot HC\)
\(\Leftrightarrow BH^2=2\cdot6=12\)
hay \(BH=2\sqrt{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔBHA vuông tại H, ta được:
\(BA^2=BH^2+HA^2\)
\(\Leftrightarrow AB^2=\left(2\sqrt{3}\right)^2+2^2=12+4=16\)
hay BA=4(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại B, ta được:
\(AC^2=BA^2+BC^2\)
\(\Leftrightarrow BC^2=8^2-4^2=48\)
hay \(BC=4\sqrt{3}\left(cm\right)\)
13 tháng 7 2021
b) Xét ΔABC vuông tại B có
\(\sin\widehat{A}=\dfrac{BC}{CA}=\dfrac{4\sqrt{3}}{8}=\dfrac{\sqrt{3}}{2}\)
\(\cos\widehat{A}=\dfrac{BA}{CA}=\dfrac{4}{8}=\dfrac{1}{2}\)
TD
0
23 tháng 7 2021
Bài 3:
Ta có: a//b
nên \(x+y=180\)
mà \(2x-3y=0\)
nên \(\left\{{}\begin{matrix}x+y=180\\2x-3y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+2y=180\\2x-3y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5y=180\\x+y=180\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=36\\x=144\end{matrix}\right.\)
TN
2
19 tháng 12 2021
Câu 4:
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
19 tháng 12 2021
Câu 1:
\(a,=\dfrac{1}{2}+9\cdot\dfrac{1}{9}-18=\dfrac{1}{2}+1-18=-\dfrac{33}{2}\\ b,=2-1+4\cdot\dfrac{1}{4}+9\cdot\dfrac{1}{9}\cdot9=1+1+9=11\\ c,=-21,3\left(54,6+45,4\right)=-21,3\cdot100=-2130\\ d,B=\left(\dfrac{1}{16}+\dfrac{1}{2}-\dfrac{1}{16}\right):\left(\dfrac{1}{8}-\dfrac{1}{8}+1\right)=\dfrac{1}{2}:1=\dfrac{1}{2}\)
H9
HT.Phong (9A5)
CTVHS
2 tháng 10 2023
Bài 5:
a) \(x^2-xy+x-y\)
\(=\left(x^2-xy\right)+\left(x-y\right)\)
\(=x\left(x-y\right)+\left(x-y\right)\)
\(=\left(x+1\right)\left(x-y\right)\)
b) \(xz+yz+4x+4y\)
\(=\left(xz+yz\right)+\left(4x+4y\right)\)
\(=z\left(x+y\right)+4\left(x+y\right)\)
\(=\left(z+4\right)\left(x+y\right)\)
c) \(x^2-x-y^2+y\)
\(=\left(x^2-y^2\right)-\left(x-y\right)\)
\(=\left(x+y\right)\left(x-y\right)-\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y-1\right)\)
d) \(x^2+2x+2z-z^2\)
\(=\left(x^2-z^2\right)+\left(2x+2z\right)\)
\(=\left(x+z\right)\left(x-z\right)+2\left(x+z\right)\)
\(=\left(x+z\right)\left(x-z+2\right)\)
SV
Sinh Viên NEU
CTVVIP
16 tháng 10 2023
1 poverty
2 decision
3 worried
4 awake
5 singers
7 northen
8 disappeared
9 difference
10 unimportant
11 windy
12 portable
13 sensibly
14 painting
15 mainly