Tìm số dư khi chia tổng:A=1+5+52+...+52008 cho 6, cho 31
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MH
28 tháng 12 2021
\(B=3+3^2+3^3+3^4+...+3^{2009}+3^{2010}\)
\(=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{2009}+3^{2010}\right)\)
\(=3\left(1+3\right)+3^3\left(1+3\right)+...+3^{2009}\left(1+3\right)\)
\(=4.\left(3+3^3+...+3^{2009}\right)\)
⇒ \(B\) ⋮ 4
29 tháng 12 2021
b: \(C=5\left(1+5+5^2\right)+...+5^{2008}\left(1+5+5^2\right)=31\cdot\left(5+...+5^{2008}\right)⋮31\)
AH
Akai Haruma
Giáo viên
13 tháng 12 2022
Lời giải:
a. $(x-3)(y+1)=5=1.5=5.1=(-1)(-5)=(-5)(-1)$
Vì $x-3, y+1$ cũng là số nguyên nên ta có bảng sau:
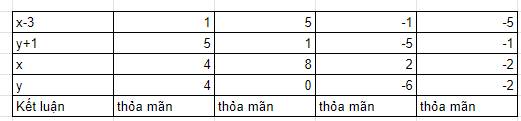
b.
$A=21+5+(5^2+5^3)+(5^4+5^5)+....+(5^{98}+5^{99})$
$=26+5^2(1+5)+5^4(1+5)+....+5^{98}(1+5)$
$=2+24+(1+5)(5^2+5^4+...+5^{98}$
$=2+24+6(5^2+5^4+....+5^{98})=2+6(4+5^2+5^4+...+5^{98})$
$\Rightarrow A$ chia $6$ dư $2$.
NT
1
20 tháng 8 2015
Gọi tổng là S
\(S=1+\left(5+5^2\right)+\left(5^3+5^4\right)+...+\left(5^{2007}+5^{2008}\right)\)
\(S=1+5.6+5^3.6+....+5^{2007}.6\)
\(S=1+6.\left(5+5^3+...+5^{2007}\right)\)
Vậy S chia 6 dư 1
\(S=\left(1+5+5^2\right)+\left(5^3+5^4+5^5\right)+....+\left(5^{2006}+5^{2007}+5^{2008}\right)\)
\(S=31.1+31.5^3+....+31.5^{2007}\)
\(S=31.\left(1+5^3+....+5^{2007}\right)\)
Vậy S chia hết cho 31 hay S chia 31 dư 0
DD
2
16 tháng 5 2019
Tổng có 2008 số hạng. Ta có :
1 + 5 + 52 + ... + 52008
= 1 + 5 + ( 52 + 53 + 54 ) + ( 56 + 57 + 58 ) + ... + ( 52006 + 52007 + 52008 )
= 1 + 5 + 52( 1 + 5 + 52 ) + 55( 1 + 5 + 52 ) + ... + 52006( 1 + 5 + 52 )
= 6 + 52 . 31 + 55 . 31 + ... + 52006 . 31
= 6 + 31( 52 + 55 + ... + 52006 ) chia cho 31 dư 6
#ĐinhBa
KN
16 tháng 5 2019
Đặt \(A=1+5+5^2+5^3+...+5^{2008}\)
A có 2009 số chia làm 1004 cặp, còn dư số 1
\(\Rightarrow A=1+\left(5+5^2\right)+\left(5^3+5^4\right)+...+\left(5^{2007}+5^{2008}\right)\)
\(\Rightarrow A=1+5\left(1+5\right)+5^3\left(1+5\right)+...+5^{2007}\left(1+5\right)\)
\(\Rightarrow A=1+5.6+5^3.6+...+5^{2007}.6\)
\(\Rightarrow A=1+6\left(5+5^3+...+5^{2007}\right)\)
Vậy A chia 6 dư 1.
TP
0
NN
1