Chứng minh \(\dfrac{1}{5}\)< \(\dfrac{1}{4^2}\)+\(\dfrac{1}{5^2}\)+\(\dfrac{1}{6^2}\)+\(\dfrac{1}{7^2}\)+......+\(\dfrac{1}{99^2}\)+\(\dfrac{1}{100^2}\)<\(\dfrac{1}{3}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


S=(1/31+1/32+...+1/40)+(1/41+...+1/50)+(1/51+...+1/60)
=>S>1/40*10+1/50*10+1/60*10=3/5
S=(1/31+1/32+...+1/40)+(1/41+...+1/50)+(1/51+...+1/60)
=>S<1/30*10+1/40*10+1/50*10=4/5
=>3/5<S<4/5

Đặt \(A=\dfrac{1}{5^2}+\dfrac{1}{6^2}+...+\dfrac{1}{2014^2}\)
\(A>\dfrac{1}{5^2}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+...+\dfrac{1}{2014.2015}\)
\(A>\dfrac{1}{5^2}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+...+\dfrac{1}{2014}-\dfrac{1}{2015}\)
\(A>\dfrac{1}{5^2}+\dfrac{1}{6}-\dfrac{1}{2015}\)
\(A>\dfrac{1}{5^2}+\dfrac{1}{6}-\dfrac{1}{150}=\dfrac{1}{5}\) (đpcm)

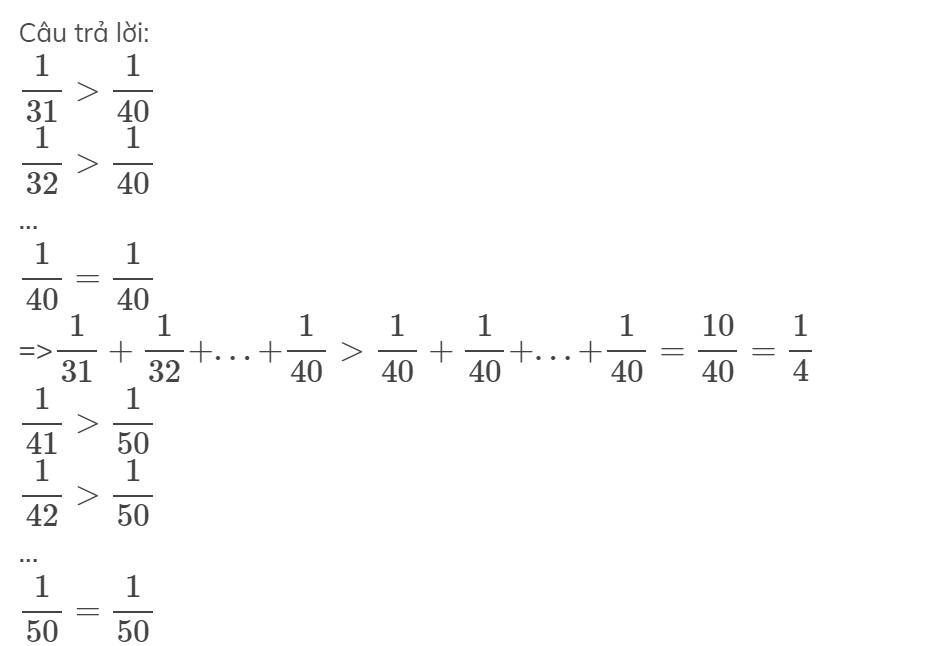
\(\dfrac{1}{31}>\dfrac{1}{40}\)
\(\dfrac{1}{32}>\dfrac{1}{40}\)
...
\(\dfrac{1}{40}=\dfrac{1}{40}\)
=>\(\dfrac{1}{31}+\dfrac{1}{32}+...+\dfrac{1}{40}>\dfrac{1}{40}+\dfrac{1}{40}+...+\dfrac{1}{40}=\dfrac{10}{40}=\dfrac{1}{4}\)
\(\dfrac{1}{41}>\dfrac{1}{50}\)
\(\dfrac{1}{42}>\dfrac{1}{50}\)
...
\(\dfrac{1}{50}=\dfrac{1}{50}\)
=>\(\dfrac{1}{41}+\dfrac{1}{42}+...+\dfrac{1}{50}>\dfrac{1}{50}+\dfrac{1}{50}+...+\dfrac{1}{50}=\dfrac{10}{50}=\dfrac{1}{5}\)
\(\dfrac{1}{51}>\dfrac{1}{60}\)
\(\dfrac{1}{52}>\dfrac{1}{60}\)
...
\(\dfrac{1}{60}=\dfrac{1}{60}\)
=>\(\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{60}>\dfrac{1}{60}+\dfrac{1}{60}+...+\dfrac{1}{60}=\dfrac{10}{60}=\dfrac{1}{6}\)
=>\(S>\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}=\dfrac{3}{5}\)
\(\dfrac{1}{31}< \dfrac{1}{30}\)
\(\dfrac{1}{32}< \dfrac{1}{30}\)
...
\(\dfrac{1}{40}< \dfrac{1}{30}\)
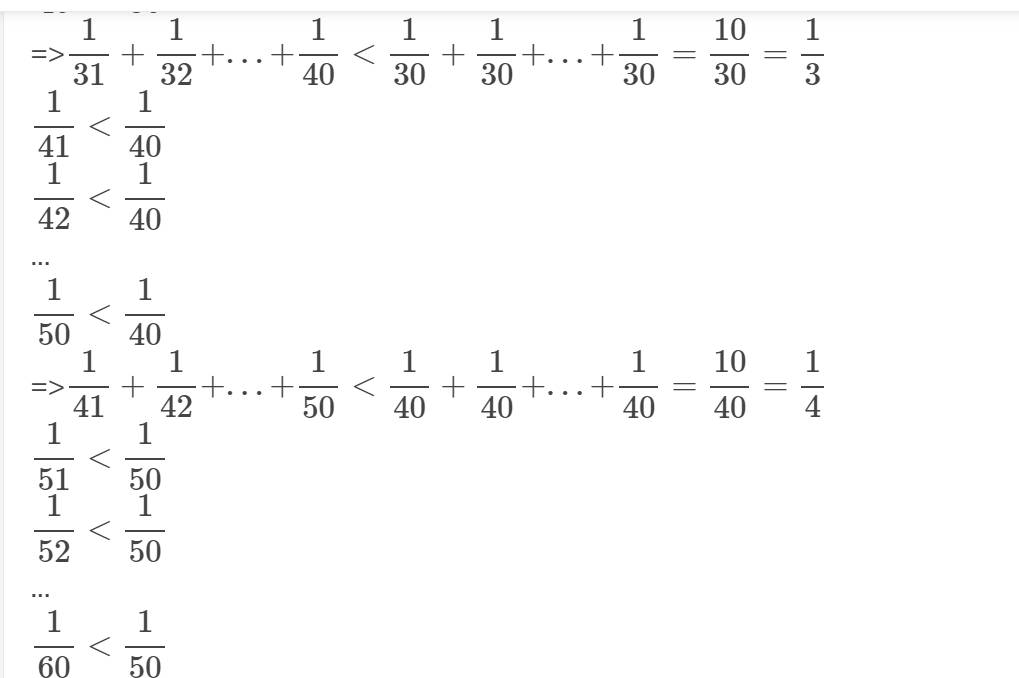
=>\(\dfrac{1}{31}+\dfrac{1}{32}+...+\dfrac{1}{40}< \dfrac{1}{30}+\dfrac{1}{30}+...+\dfrac{1}{30}=\dfrac{10}{30}=\dfrac{1}{3}\)
\(\dfrac{1}{41}< \dfrac{1}{40}\)
\(\dfrac{1}{42}< \dfrac{1}{40}\)
...
\(\dfrac{1}{50}< \dfrac{1}{40}\)
=>\(\dfrac{1}{41}+\dfrac{1}{42}+...+\dfrac{1}{50}< \dfrac{1}{40}+\dfrac{1}{40}+...+\dfrac{1}{40}=\dfrac{10}{40}=\dfrac{1}{4}\)
\(\dfrac{1}{51}< \dfrac{1}{50}\)
\(\dfrac{1}{52}< \dfrac{1}{50}\)
...
\(\dfrac{1}{60}< \dfrac{1}{50}\)
=>\(\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{60}< \dfrac{1}{50}+\dfrac{1}{50}+...+\dfrac{1}{50}=\dfrac{10}{50}=\dfrac{1}{5}\)
=>\(S< \dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}=\dfrac{4}{5}\)
=>\(\dfrac{3}{5}< S< \dfrac{4}{5}\)

1/31>1/40
1/32>1/40
...
1/40=1/40
=>1/31+1/32+...+1/40>1/40*10=1/4
1/41>1/50
1/42>1/50
...
1/50=1/50
=>1/41+1/42+...+1/50>10/50=1/5
1/51>1/60
1/52>1/60
...
1/60=1/60
=>1/51+1/52+...+1/60>10/60=1/6
=>S>1/4+1/5+1/6=3/5
1/31<1/30
1/32<1/30
...
1/40<1/30
=>1/31+1/32+...+1/40<1/30*10=1/3
1/41<1/40
1/42<1/40
...
1/50<1/40
=>1/41+1/42+...+1/50<10/40=1/4
1/51<1/50
1/52<1/50
...
1/60<1/50
=>1/51+1/52+...+1/60<10/50=1/5
=>S<1/3+1/4+1/5=4/5



\(\dfrac{1}{13}-\dfrac{1}{18}=\dfrac{18}{13.18}-\dfrac{13}{13.18}=\dfrac{18-13}{13.18}=\dfrac{5}{13.18}\)
\(\dfrac{5}{13\cdot18}=\dfrac{18}{13\cdot18}-\dfrac{13}{13\cdot18}=\dfrac{1}{13}-\dfrac{1}{18}\)(đpcm)
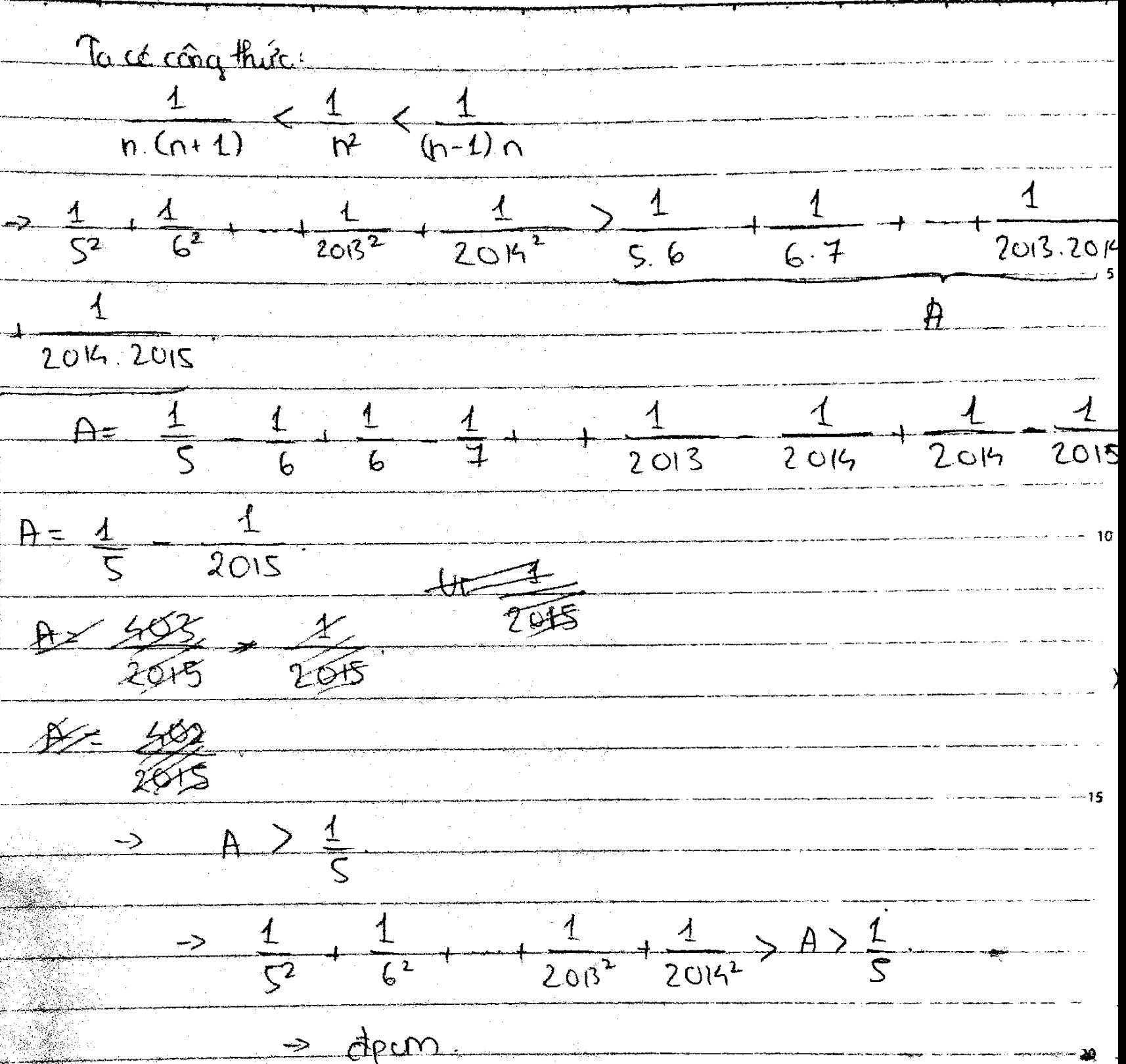

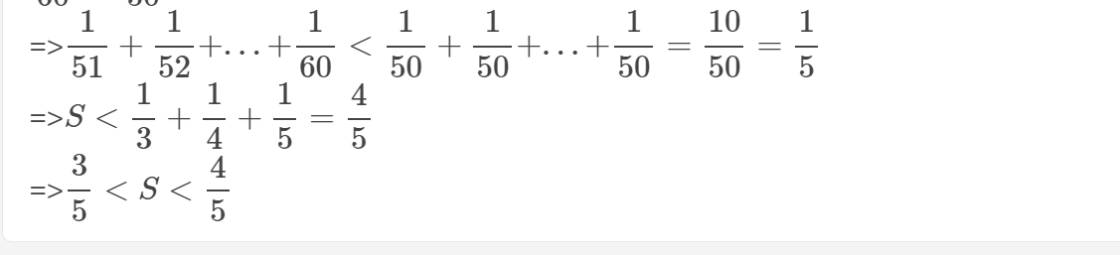
\(\dfrac{1}{4^2}+\dfrac{1}{5^2}+...+\dfrac{1}{100^2}>\dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+...+\dfrac{1}{100\cdot101}=\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{100}-\dfrac{1}{101}=\dfrac{1}{4}-\dfrac{1}{101}>\dfrac{1}{4}-\dfrac{1}{20}=\dfrac{1}{5}\left(1\right)\)
\(\dfrac{1}{4^2}+\dfrac{1}{5^2}+...+\dfrac{1}{100^2}< \dfrac{1}{3\cdot4}+\dfrac{1}{4\cdot5}+...+\dfrac{1}{99\cdot100}=\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{100}=\dfrac{1}{3}-\dfrac{1}{100}< \dfrac{1}{3}\left(2\right)\) Từ (1) và (2) \(\Rightarrow\dfrac{1}{5}< \dfrac{1}{4^2}+\dfrac{1}{5^2}+...+\dfrac{1}{99^2}+\dfrac{1}{100^2}< \dfrac{1}{3}\)