Tìm x,y,z biết rằng:x2+y2+z2=x+y+z
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\) ⇒ \(\dfrac{x^2}{a^2}=\dfrac{y^2}{b^2}=\dfrac{z^2}{c^2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x^2}{a^2}\) = \(\dfrac{y^2}{b^2}\) = \(\dfrac{z^2}{c^2}\) = \(\dfrac{x^2+y^2+z^2}{a^2+b^2+c^2}\) = \(\dfrac{x^2+y^2+z^2}{1}\) = \(x^2+y^2+z^2\) (1)
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}=\dfrac{x+y+z}{a+b+c}\) = \(\dfrac{x+y+z}{1}\) = \(x+y+z\)
\(\dfrac{x}{a}\) = \(x+y+z\) ⇒ \(\dfrac{x^2}{a^2}\) = (\(x+y+z\))2 (2)
Từ (1) và (2) ta có :
\(\dfrac{x^2}{a^2}\) = \(x^2\) + y2 + z2 = ( \(x+y+z\))2 (đpcm)
ax=by=cz ⇒ �2�2=�2�2=�2�2a2x2=b2y2=c2z2
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
�2�2a2x2 = �2�2b2y2 = �2�2c2z2 = �2+�2+�2�2+�2+�2a2+b2+c2x2+y2+z2 = �2+�2+�211x2+y2+z2 = �2+�2+�2x2+y2+z2 (1)
��=��=��ax=by=cz Áp dụng tính chất dãy tỉ số bằng nhau ta có:
��=��=��=�+�+��+�+�ax=by=cz=a+b+cx+y+z = �+�+�11x+y+z = �+�+�x+y+z
��ax = �+�+�x+y+z ⇒ �2�2a2x2 = (�+�+�x+y+z)2 (2)
Từ (1) và (2) ta có :
�2�2a2x2 = �2x2 + y2 + z2 = ( �+�+�x+y+z)2 (đpCm)

Ta có : \(x^2+y^2\ge2xy\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge\left(x+y\right)^2\)
\(\Leftrightarrow x^2+y^2\ge\frac{\left(x+y\right)^2}{2}\)
Áp dụng vào bài toán có :
\(P\le\frac{x+y}{\frac{\left(x+y\right)^2}{2}}+\frac{y+z}{\frac{\left(y+z\right)^2}{2}}+\frac{z+x}{\frac{\left(z+x\right)^2}{2}}\) \(=\frac{2}{x+y}+\frac{2}{y+z}+\frac{2}{z+x}=\frac{1}{2}\left(\frac{4}{x+y}+\frac{4}{y+z}+\frac{4}{z+x}\right)\)
Áp dụng BĐT Svacxo ta có :
\(\frac{4}{x+y}\le\frac{1}{x}+\frac{1}{y}\), \(\frac{4}{y+z}\le\frac{1}{y}+\frac{1}{z}\), \(\frac{4}{z+x}\le\frac{1}{z}+\frac{1}{x}\)
Do đó : \(P\le\frac{1}{2}\left[2.\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\right]=2016\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=z=\frac{1}{672}\)
P/s : Dấu "=" không chắc lắm :))





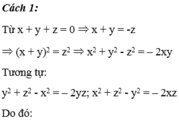
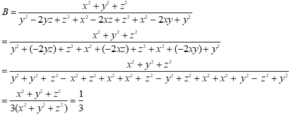
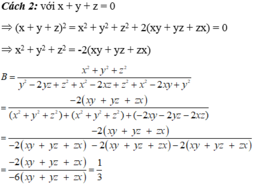
Từ trên => \(x^2=x\); \(y^2=y\); \(z^2=z\)
=> phân tích ra thì ta có 2 kết quả
x=y=z=0 và x=y=z=1