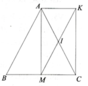
Câu 9:Cho tam giác ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của
AC, K là điểm đối xứng với M qua I. Tứ giác AMCK là hình gì?
A. Hình chữ nhật
B. Hình thoi
C. Hình vuông
D. Cả A, B, C đều sai
Câu 10: Hãy chọn câu sai.
A. Tứ giác có 4 cạnh bằng nhau là hình thoi
B. Tứ giác có hai đường chéo vuông góc với nhau và bằng nhau là hình thoi
C. Hình bình hành có đường chéo là phân giác của một góc là hình thoi
D. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tứ giác AMCK là hcn vì
AI=IC(I là trung điểm của AC)
IM=IK(K là điểm đối xứng vs M qua I)
=>Tứ giác AMCK là hình bình hành(DHNB số 5)
Xét tứ giác AMCK có góc M vuông
=> Hình bình hành AMCK là hcn
Tứ giác ACMB là hình bình hành vì
Ta có Bm ss AK (MC ss AK theo tính chắt hcn)
Xét tam giác ABC có BM=MC,AI=IC
=>IM là đường trung bình của tam giác ABC
=>IM ss Ab
Mà I nằm giữa M và K =>MK ss AB
=>ABMK là hình bình hành (DHNB số 1)
Vì AMCk là hcn nên chỉ cần MI vuông góc CA là hình vuông

a) Xét tứ giác AMCK:
I là trung điểm của AC (gt).
I là trung điểm của MK (K là điểm đối xứng với M qua I).
Mà \(\widehat{AMC}=90^o\left(AM\perp BC\right).\)
=> Tứ giác AMCK là hình chữ nhật (dhnb).
b) Xét tam giác ABC cân tại A: AM là đường cao (gt).
=> AM là trung tuyến (Tính chất tam giác cân).
=> M là trung điểm của BC.
=> BM = MC.
Ta có: AK = MC (Tứ giác AMCK là hình chữ nhật).
BM = MC (cmt).
=> AK = MC = BM.
Ta có: AK // MC (Tứ giác AMCK là hình chữ nhật).
=> AK // BM.
Xét tứ giác AKMB:
AK // BM (cmt).
AK /= BM (cmt).
=> Tứ giác AKMB là hình bình hành (dhnb).
c) Tứ giác AMCK là hình vuông (gt).
=> AK = AM (Tính chất hình vuông).
Mà AK = BM (cmt).
=> AM = BM = AK.
Mà BM = \(\dfrac{1}{2}\) BC (M là trung điểm BC).
=> AM = BM = AK = \(\dfrac{1}{2}\) BC.
Xét tam giác ABC cân tại A:
AM = \(\dfrac{1}{2}\) BC (cmt).
=> Tam giác ABC vuông cân tại A.

a) Áp dụng tính chất của tam giác cân cho DABC ta có: AM ^ MC và BM = MC
I là trung điểm của AC và K đối xứng với M qua I nên tứ giác AMCK là hình bình hành
Lại có MK = AC (=2MI)
Þ Tứ giác AMCK là hình chữ nhật.
b) Vì tứ giác AMCK là hình chữ nhật (chứng minh ở a) Þ AK//MC và AK = MC = MB nên tứ giác AKMB là hình bình hành.
c) Nếu tứ giác AKMB là hình thoi thì BA = AK = KM= MB.
Þ DMBA cân tại B Þ B A M ^ = A M B ^ = 900 Þ vô lý.
Vậy không có trường hợp nào của D ABC để AKMB là hình thoi.

a: Xét tứ giác AMCK có
I là trung điểm của AC
I là trung điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
b: Để AMCK là hình vuông thì AM=CM
=>AM=BC/2
hay ΔABC vuông tại A
Câu 9:Cho tam giác ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của
AC, K là điểm đối xứng với M qua I. Tứ giác AMCK là hình gì?
A. Hình chữ nhật
B. Hình thoi
C. Hình vuông
D. Cả A, B, C đều sai
Câu 10: Hãy chọn câu sai.
A. Tứ giác có 4 cạnh bằng nhau là hình thoi
B. Tứ giác có hai đường chéo vuông góc với nhau và bằng nhau là hình thoi
C. Hình bình hành có đường chéo là phân giác của một góc là hình thoi
D. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi