Một ấm điện có ghi 220V-1000W được sử dụng với hiệu điện thế 220V để đun 3lnước từ nhiệt độ ban đầu 300C. Hiệu suất của bếp là 60%, trong đó nhiệt lượng cung cấp để đunsôi nướccoilà có ích.a. Tính nhiệt lượng cần cung cấp để đun sôi lượng nước trên, biết nhiệt dung riêng của nước là 4200J/kg.K.b. Tính nhiệt lượng mà ấm điện đã tỏa ra khi đó.c. Tính thời gian đun sôi lượng nước trên bao nhiêu phút.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. \(Q_{thu}=mc\Delta t=2\cdot4200\cdot80=672000\left(J\right)\)
b. \(H=\dfrac{Q_{thu}}{Q_{toa}}100\%\Rightarrow Q_{toa}=\dfrac{Q_{thu}}{H}100\%=\dfrac{672000}{90}100\%\approx746666,6667\left(J\right)\)
c. \(Q_{toa}=A=Pt\Rightarrow t=\dfrac{Q_{toa}}{P}=\dfrac{746666,6667}{1000}\approx746,7\left(s\right)\)
Nhiệt lượng cần cung cấp để làm đun sôi nước:
\(Q=mc\Delta t=2\cdot4200\cdot\left(100-20\right)=672000J\)
Với hiệu suất của bếp là 90% thì nhiệt lượng bếp tỏa:
\(Q_{tp}=\dfrac{Q}{H}=\dfrac{672000}{90\%}=746666,67J\)
Thời gian cần đun sôi nước:
\(t=\dfrac{A}{P}=\dfrac{Q_{tp}}{P}=\dfrac{\dfrac{2240000}{3}}{1000}=\dfrac{2240}{3}\approx746,67s\)

a) Nhiệt lượng cần cung cấp để đun sôi lượng nước trên là:
Q1 = c.m.(T – T0) = 4200.2.(100 - 20) = 672000 (J)
b) Hiệu suất của bếp: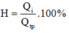
Nhiệt lượng mà ấm điện đã tỏa ra khi đó là:
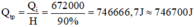
c) Từ công thức: Qtp = A = P.t
→ Thời gian đun sôi lượng nước:
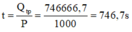
a) Nhiệt lượng cần cung cấp để đun sôi lượng nước trên là:
Q1 = c.m.(T – T0) = 4200.2.(100 - 20) = 672000 (J)
b) Hiệu suất của bếp: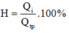

Nhiệt lượng cần cung cấp để đun sôi nước:
\(Q=mc\Delta t=3.4200.\left(100-20\right)=1008000\left(J\right)\)
Nhiệt lượng do bếp tỏa ra:
\(H=\dfrac{Q_{thu}}{Q_{tỏa}}\Rightarrow Q_{tỏa}=\dfrac{Q_{thu}}{H}=\dfrac{1008000}{80\%}=1260000\left(J\right)\)
c) \(1000W=1kW\)
Điện năng bếp tiêu thụ trong 1 tháng:
\(A=P.t=1.26.5=130\left(kWh\right)\)
Tiền điện phải trả: \(130.1300=169000\left(đ\right)\)
mong mọi người giúp mình giải
a. \(Q_{thu}=mc\Delta t=3\cdot4200\cdot70=88200\left(J\right)\)
b. \(H=\dfrac{Q_{thu}}{Q_{toa}}100\%=>Q_{toa}=\dfrac{Q_{thu}}{H}100\%=\dfrac{88200}{60}100\%=147000\left(J\right)\)
c. \(Q_{toa}=A=Pt=>t=\dfrac{A}{P}=\dfrac{147000}{1000}=147\left(s\right)\)