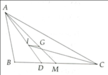
cho tam giác ABC có AB+AC=2BC. Gọi I, G lần lượt là giao điểm của các đường phân giác và trọng tâm tam giác ABC. Chứng minh IG song song với BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 7 2017
1/. _Kẻ pg AD và đ/cao AE (D ; E thuộc BC) ta thấy AG/AE=2/3_bt:(1)
Trong tg ABC vớí pg AD ta có : DB/DC= AB/AC=6/12=1/2 <=> BD=3 ; DC=6 (cm)
Trong tg ABD với pg BI ta có : IA/IB=AB/BD =3/6 <=>AI/AD=2/3 -bt:(2). từ (1) & (2)suy ra đpcm
góc AED=^ACB=48 độ ( hai góc đều cọng với góc^BED thì =180 độ
HS
11 tháng 3 2017
a) Gọi IP, IQ, IS lần lượt là khoảng cách từ I đến BC, CA, AB => IP = IQ = IS
Ta có SABC = SBIC +SAIC +SAIB = 1/2.IP.BC +1/2.IQ.AC +1/2.IS.AB =1/2.IP(BC +CA +AB) = 1/2.IP.3BC( vì AB + AC = 2BC) = 3SBIC
b) Gọi D, M lần lượt là giao điểm của AI, AG với BC.
Trong tam giác ABC có AD là phân giác => \(\frac{AC}{DC}=\frac{AB}{DB}=\frac{AB+AC}{DC+DB}=\frac{AB+AC}{BC}=2\)2
Trong tam giác ABD có BI là phân giác => \(\frac{AI}{ID}=\frac{AB}{DB}=2\)
Mặt khác do G là trọng tâm tg ABC => \(\frac{AG}{GM}=2\)
=> \(\frac{AI}{ID}=\frac{AG}{GM}\)=> IG //BC (Talet đảo)
14 tháng 7 2023
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/2=CD/3=(BD+CD)/(2+3)=15/5=3
=>BD=6cm và CD=9cm
Xét ΔBAD có BI là phân giác
nên AI/ID=AB/BD=2
=>AI/AD=2/3=AG/AM
=>IG//BC
14 tháng 7 2023
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/2=CD/3=(BD+CD)/(2+3)=15/5=3
=>BD=6cm và CD=9cm
Xét ΔBAD có BI là phân giác
nên AI/ID=AB/BD=2
=>AI/AD=2/3=AG/AM
=>IG//BC