Cho tam giác ABC có 3 góc đều nhọn. vẽ AH vuông góc vói BC tại H . Trên tia đối của tia HA lấy điểm D sao cho HA=HD
1) Chứng minh CA=CD
2) Vẽ HM⊥AC tại M;HN⊥DC tại N.Chứng minh: HC là tia phân giác của góc
MHN
3) Chứng minh HC là đường trung trực của MN
4) Xác định vị trí điểm H trên cạnh BC để AB//CD
Giúp câu 3 và câu 4 với!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xét ΔCAD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAD cân tại C
hay CA=CD
giúp em khúc 2,3,4 với ạ; tất cả đều cùng 1 bài
1 thì em chưa học đến tam giác cân

1: Xét ΔHAC vuông tại H và ΔHDC vuông tại H có
CH chung
HA=HD
Do đó: ΔHAC=ΔHDC
Suy ra: CA=CD

1: Xét ΔCAD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAD cân tại C
hay CA=CD

1: Xét ΔCAD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAD cân tại C
hay CA=CD

Vẽ nháp bằng tay, hình không đẹp cho lắm :v Bài viết có hơi lỗi.
Bài toán phụ : Chứng minh tam giác vuông có 1 góc 60 độ thì cạnh góc vuông nhỏ hơn sẽ bằng 1 nửa cạnh huyền.
Tam giác MNP vuông tại M có góc N là 60 độ.

Trên tia đối tia MN lấy điểm Q sao cho MQ=MN
Tam giác NPQ có PM vừa là trung tuyến vừa là đường cao nên cân tại P, mà lại có 1 góc 60 độ nên là tam giác đều ( Dấu hiệu nhận biết tam giác đều), từ đó suy ra NQ = NP, mà NQ= 2MN nên MN = \(\frac{1}{2}\)NP, bài toán được chứng minh.
Tương tự với bài toán của chúng ta :

\(\Delta ABC\)vuông tại Acó \(\widehat{B}=60^o\) \(\Rightarrow AB=\frac{1}{2}BC\)
\(\Delta ABH\)vuông tại H có \(\widehat{B}=60^o\) \(\Rightarrow HB=\frac{1}{2}AB\)
\(\Rightarrow HB=\frac{1}{4}BC\)
Trước hết \(\Delta ABH\) vuông tại H có \(\widehat{B}=60^o\)
nên \(\widehat{HAB}=90^o-60^o=30^o\)Mà \(\widehat{DAH}+\widehat{HAB}=\widehat{BAC}=90^o\)
\(\Rightarrow\widehat{DAH}=60^o\)
\(\Delta DAH\)cân tại A ( AD = AH ), có góc DAH là 60o nên là tam giác đều ( Dấu hiệu nhận biết tam giác đều )
Như vậy AI là đường cao đồng thời cũng là phân giác góc DAH
\(\Rightarrow\widehat{IAH}=\frac{1}{2}\widehat{DAH}=\frac{60^o}{2}=30^o\)
\(\Rightarrow\widehat{KAB}=\widehat{IAH}+\widehat{HAB}=30^o+30^o=60^o\)
\(\Delta KAB\)có \(\widehat{KAB}=\widehat{KBA}=60^o\) nên là tam giác đều
\(\Rightarrow KB=AB\)
Mà \(HB=\frac{1}{2}AB\Rightarrow HB=\frac{1}{2}KB\), hay H là trung điểm của KB.
Vậy ....

Ta có :O là trung điểm của BC(gt)
O là trung điểm của AK(OA=OK)
=>ABKC là hình bình hành(dhnb)
Mà góc BAC = 90 độ
=>ABKC là hình chữ nhật (dhnb)
=>AB=CK và góc ACK = 90 độ
Xét tam giác ABC và tam giác CKA có:
AB=CK(cmt)
góc BAC=góc KCA( cùng bằng 90 độ)
AC chung
Vậy tam giác ABC = tam giác CKA(c.g.c)
b)Xét tam giác AHB và tam giác CHA có
góc AHB = góc CHA (=90 độ)
góc BAH =góc ACH(cùng phụ với góc B)
Vậy tam giác AHB đồng dạng tam giác CHA(g.g)
=>\(\dfrac{AB}{AH}=\dfrac{AC}{CH}\)(1)
Ta có AH\(\perp\)CH
ED\(\perp\)CH
=>AH//DE
Xét tam giác ACH có
AH//DE
=>\(\dfrac{AE}{HD}=\dfrac{AC}{CH}\)
=>\(\dfrac{AE}{AH}=\dfrac{AC}{CH}\)(do AH=AD)(2)
Từ(1) và (2) => \(\dfrac{AB}{AH}=\dfrac{AE}{AH}\)
=>AB=AE(đpcm)

a: Xét ΔAHB vuông tại H và ΔAHE vuông tại H có
AH chung
HB=HE
Do đó: ΔAHB=ΔAHE
b: Xét tứ giác ABDE có
H là trung điểm của AD
H là trung điểm của BE
Do đó: ABDE là hình bình hành
Suy ra: DE//AB
c: Xét ΔEAD có
EH là đường cao
EH là đường trung tuyến
Do đó: ΔEAD cân tại E
Xét ΔCAD có
CH là đường cao
CH là đường trung tuyến
DO đó: ΔCAD cân tại C
Xét ΔEAC và ΔEDC có
EA=ED
EC chung
AC=DC
Do đó: ΔEAC=ΔEDC
Suy ra: \(\widehat{EAC}=\widehat{EDC}\)
GT,KL tự viết (hình cũng tự vẽ)
a, Xét △AHB và △AHE có :
AH : chung
\(\widehat{AHB}=\widehat{AHE}(=90^o)\)
HB = HE (GT)
=> △AHB = △AHE (c.g.c)
b, Xét △AHB và △DHE có :
AH = DH(GT)
\(\widehat{AHB}=\widehat{DHE}(=90^o)\)
BH = EH (GT)
=> △AHB = △DHE (c.g.c)
=> \(\widehat{HAB}=\widehat{HDE}\) (2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
=> DE // AB
c, Xét △AHC và △DHC có :
HC : chung
\(\widehat{AHC}=\widehat{DHC}(=90^o)\)
AH = DH (GT)
=> △AHC = △DHC (c.g.c)
=> AC = DC (2 cạnh tương ứng)
\(\widehat{ACH}=\widehat{DCH}\) (2 góc tương ứng)
Xét △EAC và △EDC có :
EC : chung
\(\widehat{ECA}=\widehat{ECD}(cmt)\)
AC = DC (cmt)
=> △EAC = △EDC (c.g.c)
=> \(\widehat{EAC}=\widehat{EDC}\) (2 góc tương ứng)
d, Vì MN // AD => \(\dfrac{ME}{DE}=\dfrac{MN}{AD}\)
Xét △MEN và △DEA có :
\(\dfrac{ME}{DE}=\dfrac{MN}{AD} (cmt)\)
\(\widehat{EMN}=\widehat{EDA}( so le)\)
=> △MEN = △DEA (c.g.c)
=> \(\widehat{MEN}=\widehat{DEA}\) (2 góc tương ứng)
Mà 2 góc ở vị trí đối đỉnh với nhau
=> A , E , N thẳng hàng
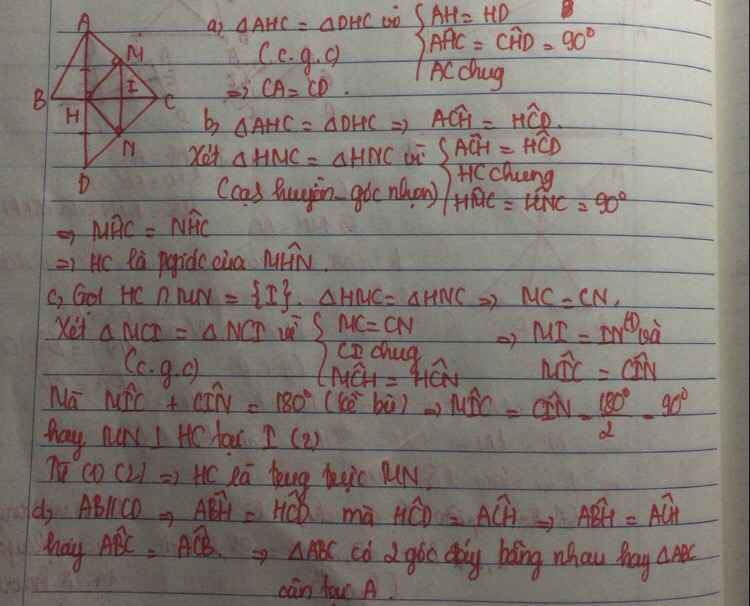
1: Xét ΔCAD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAD cân tại C
Help me