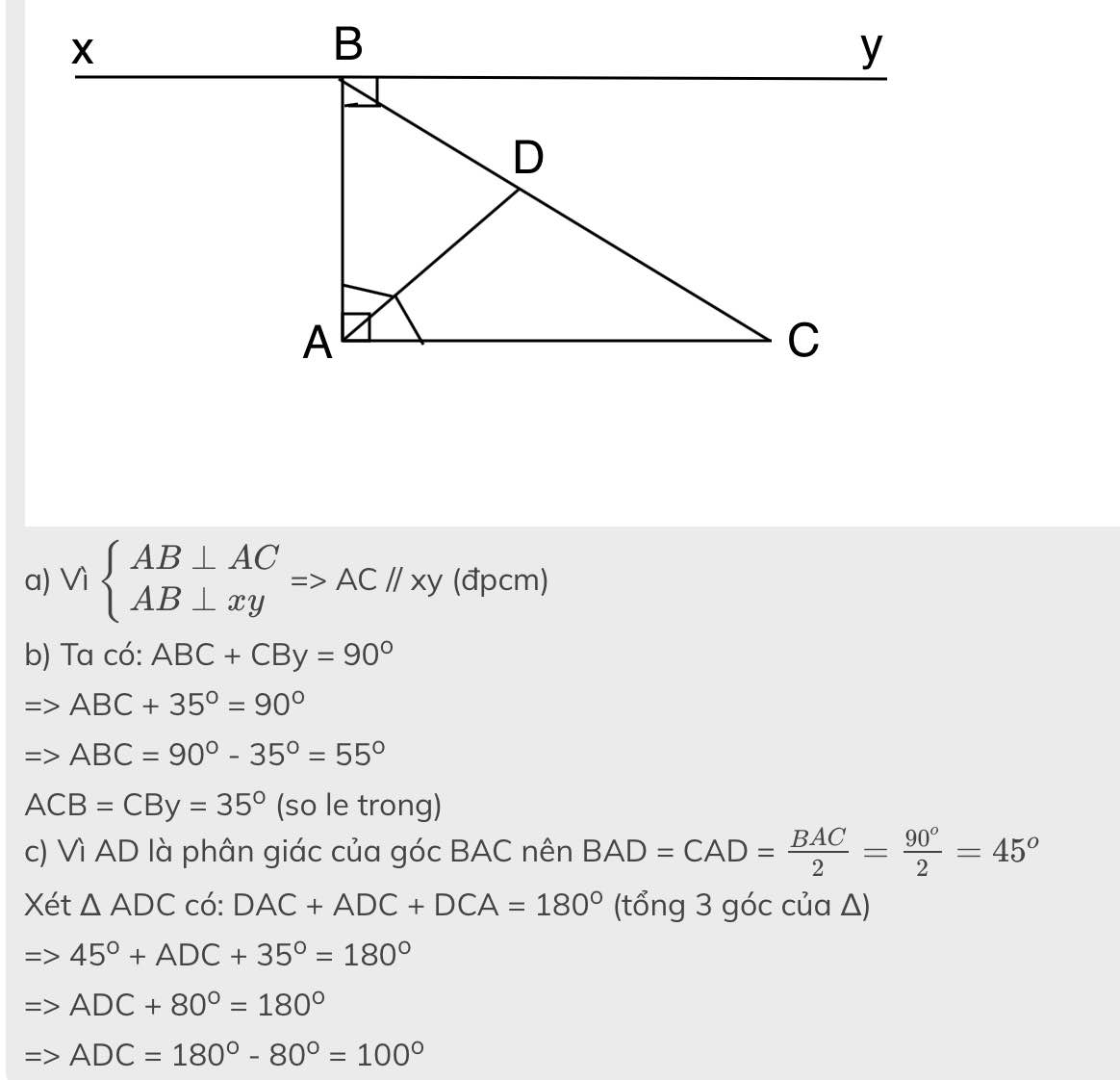
Cho tam giác ABC có ⌢ A = 90 0 . Qua đỉnh B của tam giác kẻ đường thẳng xy vuông góc với cạnh AB ( AC, By thuộc cùng một nửa mặt phẳng có bờ là đường thẳng chứa cạnh AB). a) Chứng minh xy // AC. b) Biết góc C ⌢ B y = 35 0 . Tính số đo các góc còn lại của tam giác ABC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 8 2016
1)
a) Ta có: góc BAD+góc CAE+góc BAC=180 độ
Mà góc BAC=90 độ nên góc BAD+ góc CAE=90 độ (1)
Vì tam giác ACE vuông tại E nên góc ACE+góc CAE=90 độ(2)
Từ (1) và (2) => góc BAD= góc ACE
Xét tam giác ABD và tam giác ACE có:
góc ADB=góc AED=90 độ
AB=AC ( vì tam giác ABC vuông cân tại A)
góc BAD=góc ACE (cmt)
=> tam giác ABD=tam giác ACE (cạnh huyền-góc nhọn)
b) Theo câu a) Tam giác ABD=tam giác ACE
=> DA=EC và BD=AE
Mà DE=DA+AE nên DE=EC+BD
25 tháng 1 2019
Bài 1:
Độ dài cạnh AB: ( 49 + 7 ) : 2 = 28 (cm)
Độ dài cạnh AC: 28 - 7 = 21 (cm)
Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A có:
\(BC^2=AC^2+AB^2\)
Hay \(BC^2=21^2+28^2\)
\(\Rightarrow BC^2=441+784\)
\(\Rightarrow BC^2=1225\)
\(\Rightarrow BC=35\left(cm\right)\)
25 tháng 1 2019
Bài 2:
Áp dụng định lý Py-ta-go vào tam giác ABD vuông tại D có:
\(AB^2=AD^2+BD^2\)
\(\Rightarrow AD^2=AB^2-BD^2\)
Hay \(AD^2=17^2-15^2\)
\(\Rightarrow AD^2=289-225\)
\(\Rightarrow AD^2=64\)
\(\Rightarrow AD=8\left(cm\right)\)
Trong tam giác ABC có:
\(AD+DC=AC\)
\(\Rightarrow DC=AC-AD=17-8=9\left(cm\right)\)
Áp dụng định lý Py-ta-go vào tam giác BCD vuông tại D có:
\(BC^2=BD^2+DC^2\)
Hay \(BC^2=15^2+9^2\)
\(\Rightarrow BC^2=225+81\)
\(\Rightarrow BC^2=306\)
\(\Rightarrow BC=\sqrt{306}\approx17,5\left(cm\right)\)
VT
1 tháng 11 2018
Giải
Bạn cân hình cho vuông góc nha! Mình không cân được.
Hai tia AE và AC cùng thuộc nửa mặt phẳng có bờ là đường thẳng AB và \(\widehat{BAC}< \widehat{BAE}=90^o\)nên tia AC nằm giữa hai tia AB và AE .
Do đó :
\(\widehat{BAC}+\widehat{CAE}=\widehat{BAE}\)hay
\(\widehat{BAC}=90^o-\widehat{CAE}\left(1\right)\)
Tương tự ta cũng có :
\(\widehat{EAD}-90^o-\widehat{CAE}\left(2\right)\)
Từ (1) và (2) suy ra :
\(\widehat{BAC}=\widehat{EAD}\left(3\right)\)
Xét 2 tam giác ABC và EAD,chúng có :
\(AB=AE\left(gt\right),\widehat{BAC}=\widehat{EAD}\left(theo\left(3\right)\right),AC=AD\left(gt\right)\)
Vậy \(\Delta ABC=\Delta AED\left(c.g.c\right)\)
b) Do 2 tam giác ABC và AED = nhau ta có :
\(BC=ED\&\widehat{C}=\widehat{D}\left(4\right)\)
Ta lại có \(CM=\frac{1}{2}BC;DN=\frac{1}{2}ED\)Vì M và N là trung điểm của BC và AD .
=> CM = AN
Hai tam giác AMC = AND có :
AC = AD (gt) \(\widehat{C}=\widehat{D}\left(theo\left(4\right)\right),CM=DN\left(theo\left(5\right)\right)\)
Vậy \(\Delta AMC=\Delta AND\left(c.g.c\right)\)
10 tháng 8 2016
![[IMG]](http://m.f16.photo.zdn.vn/upload/original/2013/12/11/16/44/994642808_1801255646_320_320.jpg)
a,Gọi P là chân đường cao hạ từ A xuống BC
Trên nửa mf bờ AF có chứa B vẽ tia Fx//AE .Trên Fx lấy Q (Q là giao của AP và Fx)
Kéo dài AB cắt EQ tại S
Ta có : \(\widehat{SQA}=\widehat{EQA}\) (FQ//AE)
\(\Rightarrow\widehat{SQA}+\widehat{QAS}=\widehat{EAQ}+\widehat{QAS}=90\)
Ta có : \(\widehat{SQA}+\widehat{QAS}+\widehat{ASQ}=180\)
\(\Rightarrow\widehat{ASQ=90^0\widehat{\Rightarrow SFA}+\widehat{FAS}=80^o}\)
Mà : \(\widehat{BAC}+\widehat{FAS}=90^o\)
=> SFA = BAC
Tương tự CM FAQ = ACB (cùng phụ PAC)
Và AF = AC
=> Tam giác AFQ = CAB
FQ = AB = AE
Chứng minh tương tự MAE = MQF (c.g.c)
=> FM = FE
> FB = EC