Một giọt nước rơi từ độ cao 45 m xuống. Hỏi sau bao lâu nó mới chạm đất?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HD
Hà Đức Thọ
Admin
30 tháng 8 2017
Gọi thời gian giọt thứ nhất rơi chạm đất là t, suy ra:
\(h=\dfrac{1}{2}gt^2\)
\(\Rightarrow 20=\dfrac{1}{2}.10.t^2\)
\(\Rightarrow t = 2s\)
Trong thời gian này, số hạt đang rơi là: \(n=\dfrac{t}{0,5}=\dfrac{2}{0,5}=4\)
VT
12 tháng 4 2019
Gọi s là quãng đường rơi của giọt nước mưa từ lúc đầu đến điểm cách mặt đất 100 m, t là thời gian rơi trên quãng đường đó, ta có : s = 1/2(g t 2 ) (1)
Mặt khác, quãng đường rơi từ lúc đầu đến mặt đất là s + 100 và thời gian rơi trên quãng đường đó là t + 1 giây.
Ta có : s + 100 = 1/2*g t + 1 2 (2)
Từ hai phương trình (1) và (2) ta rút ra : t = 100/g -0.5 ≈ 9.7(s) ⇒ s = 461(m)
Vậy, độ cao ban đầu của giọt nước mưa lúc bắt đầu rơi là:
s +100 = 561 m.
VT
23 tháng 7 2017
Chọn B.
Thời gian giọt nước rơi tới mặt đất là: t = 2 h g = 2 . 45 10 = 3 s
14 tháng 1 2022
a) Vật chạm đất sau :
\(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2.80}{10}}=4\left(s\right)\)
b) Quãng đường đi trong 3s và 4s là :
\(s_{3s}=\dfrac{1}{2}gt_{3s^2}=\dfrac{1}{2}.10.3^2=45\left(m\right)\)
\(s_{4s}=\dfrac{1}{2}gt_{4s^2}=\dfrac{1}{2}.10.4^2=80\left(m\right)\)
Quãng đường vật rơi trong giây thứ 4 :
\(\Delta s=s_{4s}-s_{3s}=80-45=35\left(m\right)\)
2 tháng 1 2021
1, Quãng đường vật đi được là: s=v.t = 50.6= 300 (km)
2, Thời gian vật chạm đất là:\(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2.45}{10}}=3\left(s\right)\)
3, Do vật chuyển động ngược dòng nước nên vận tốc của thuyền so với bờ là:
Vtb= Vtn-Vnb = 5 - 3 =2(m/s)
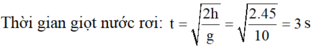
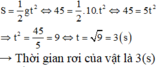
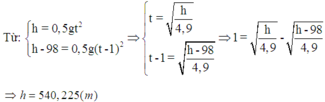
Uhm, đề thiếu rồi nhé!
3 giây nha
Thời gian giọt nước rơi tới mặt đất là: \( t = √2hg=√2.4510=3s\)