Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b)
Tam giác ABC nội tiếp đường tròn đường kính AB
=> Tam giác ABC vuông tại C
\(\Rightarrow\widehat{ACH}=\widehat{ABC}\) (cùng phụ với góc BAC)
Lại có: Góc M chung
=> ....

xét (o) có ^MTA là góc tạo bởi tt à dc chắn cung TA
^TBM là góc nt chắn cung TA
=> ^MTA = ^TBM (hq)
xét tg MTA và tg MBT có ^M chung
=> tg MTA đồng dạng tg MBT (g-g)
=> MT/MB = MA/MT
=> MT^2 = MB.MA
bài 2 tự kẻ hình đi
a, như bài 1
b, tg MAC đồng dạng tg MCB (câu a)
=> MA/MC = MC/MB
=> MC^2 = MA.MB (1)
xét tg MCO có ^MCO = 90 do MC là tt
CH _|_ MO
=> mc^2 = mh.mo (ĐL) (2)
(1)(2) => MH.MO = MA.MB
c, xét tg AHC và tg ACB có : ^ACB = ^AHC = 90(do C thuộc đường tròn đk AB)
^cah CHUNG
=> tg AHC đồng dạng tg ACB
=> ^ACH = ^CBA mà ^CBA = ^MCA (Câu a)
=> ^ACH = ^MCA
=> CA là pg...

a: Vì MC là tiếp tuyến của (O)
nen ΔOCM vuông tại C
b: Xét (O) có
góc MCA là góc tạo bởi tiếp tuyến MC và dây cung CA
góc ADC là góc nội tiếp chắn cung CA
Do đó: góc MCA=góc ADC
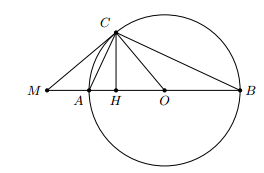


a) Ta có ˆACB=900ACB^=900 (góc nội tiếp chắn nửa đường tròn) ⇒ΔABC⇒ΔABC vuông tại C
⇒ˆABC+ˆBAC=900⇒ABC^+BAC^=900 (hai góc nhọn trong tam giác vuông) hay ˆABC+ˆHAC=900ABC^+HAC^=900
ΔAHCΔAHC vuông tại H ⇒ˆHAC+ˆACH=900⇒HAC^+ACH^=900 (hai góc nhọn trong tam giác vuông).
⇒ˆABC=ˆACH⇒ABC^=ACH^ (cùng phụ vớiˆ HACHAC^)
Lại có ˆACM=ˆABCACM^=ABC^ (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AC)
⇒ˆACM=