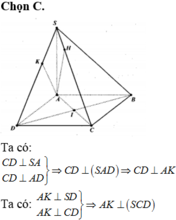
Cho hình chóp $S.ABCD$ có $SA \perp (ABCD)$. Đáy $ABCD$ là hình vuông tâm $O$. Gọi $H$, $I$, $K$ lần lượt là hình chiếu vuông góc của $A$ lên $SB$, $SC$, $SD$.
a. Chứng minh $BC \perp (SAB)$.
b. Chứng minh $AH$, $AI$, $AK$ cùng thuộc một mặt phẳng.
c. Chứng minh $HK \perp AI$.