Phương trình: (3x+4)^2=0(3x+4)22=0 có tập nghiệm...
Đọc tiếp
Phương trình: (3x+4)^2=0(3x+4)22=0 có tập nghiệm là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 3 2019
Chọn C.
Ta có :
+) 4 - 3x = 0 ⇔ x = 4/3
+) -2
x
2
+ 3x - 1 = 0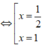 
Lập bảng xét dấu :
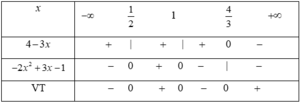
Vậy tập nghiệm của bất phương trình (4 - 3x)(-2
x
2
+ 3x - 1) ≤ 0 là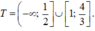 
CM
11 tháng 4 2017
a. Đúng
Vì x 2 + 1 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
4x – 8 + (4 – 2x) = 0 ⇔ 2x – 4 = 0 ⇔ 2x = 4 ⇔ x = 2
b. Đúng
Vì x 2 – x + 1 = x - 1 / 2 2 + 3/4 > 0 với mọi x nên phương trình đã cho tương đương với phương trình:
(x + 2)(2x – 1) – x – 2 = 0 ⇔ (x + 2)(2x – 2) = 0
⇔ x + 2 = 0 hoặc 2x – 2 = 0 ⇔ x = - 2 hoặc x = 1
c. Sai
Vì điều kiện xác định của phương trình là x + 1 ≠ 0 ⇔ x ≠ - 1
Do vậy phương trình 
không thể có nghiệm x = - 1
d. Sai
Vì điều kiện xác định của phương trình là x ≠ 0
Do vậy x = 0 không phải là nghiệm của phương trình 
CM
5 tháng 5 2019
Đáp án A.
Ta có: x 2 + 3x - 4 > 0 ⇔ (x - 1)(x + 4) > 0
Ta có bảng xét dấu vế trái của bất phương trình là:
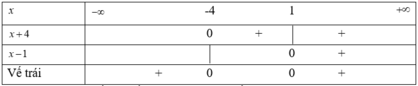
Dựa vào bảng xét dấu ta thấy, tập nghiệm của bất phương trình là: ( - ∞ ;-4) ∪ (1; + ∞ )
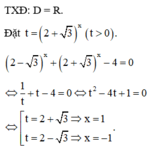
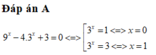
\(\left(3x+4\right)^2=0\)
\(\Leftrightarrow3x+4=0\)
\(\Leftrightarrow3x=-4\)
\(\Leftrightarrow x=\frac{-4}{3}\)
Vậy phương trình \(\left(3x+4\right)^2=0\)có tập nghiệm là \(S=\left\{\frac{-4}{3}\right\}\)