Phương trình(x+4)(9x2−1)=0 có các nghiệm là?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Ta có P T ⇔ 9 x 2 + x + 1 − 10 3 .3 x 2 + x + 1 = 0
Đặt t = 3 x 2 + x + 1 ⇒ t 2 − 10 3 t + 1 = 0
⇔ t = 3 t = 1 3 ⇒ x 2 + x + 1 = 1 x 2 + x + 1 = − 1 ⇔ x = 1 ; x = − 2 x = 0 ; x = − 1

a) Phương trình 4 x 2 + 2 x − 5 = 0
Có a = 4; b = 2; c = -5, a.c < 0
⇒ Phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-et ta có: 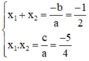
b) Phương trình . 9 x 2 − 12 x + 4 = 0
Có a = 9; b' = -6; c = 4 ⇒ Δ 2 = ( - 6 ) 2 - 4 . 9 = 0
⇒ Phương trình có nghiệm kép x 1 = x 2 .
Theo hệ thức Vi-et ta có: 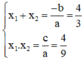
c) Phương trình 5 x 2 + x + 2 = 0
Có a = 5; b = 1; c = 2 ⇒ Δ = 1 2 − 4.2.5 = − 39 < 0
⇒ Phương trình vô nghiệm.
d) Phương trình 159 x 2 − 2 x − 1 = 0
Có a = 159; b = -2; c = -1; a.c < 0
⇒ Phương trình có hai nghiệm phân biệt x 1 ; x 2 .
Theo hệ thức Vi-et ta có: 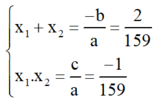

Phương trình 9x2 – 12x + 4 = 0
Có a = 9; b' = -6; c = 4 ⇒ Δ’ = (-6)2 – 4.9 = 0
⇒ Phương trình có nghiệm kép x1 = x2.
Theo hệ thức Vi-et ta có: 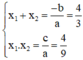

9x^2 - 32 + k^2 - 2k.x = 0
Thay x = 2 vào, ta có:
<=> 9.2^2 - 32 + k^2 - 2k.2 = 0
<=> 36 - 32 + k^2 - 4k = 0
<=> 4 + k^2 - 4k = 0
<=> (2 - k)^2 = 0
<=> 2 - k = 0
<=> k = 2

Để phương trình có hai nghiệm phân biệt thì:
\(\left(-10m\right)^2-36m>0\Leftrightarrow100m^2-36m>0\Leftrightarrow m\left(100m-36>0\right)\)
\(\Leftrightarrow m>0,36\)
Giải phương trình :
x2 - 10mx + 9m = 0
\(\Delta=0,36\Rightarrow\sqrt{\Delta}=0,6\)
<=> x1 = 5m - 0,3
x2 = 5m + 0,3
x1 - 9x2 = 0
ok , lm tiếp đi
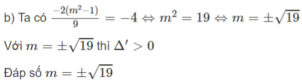


\(\left(x+4\right)\left(9x^2-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\9x^2-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x^2=\dfrac{1}{9}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=\pm\dfrac{1}{3}\end{matrix}\right.\)\(S=\left\{-4,\pm\dfrac{1}{3}\right\}\)
Ta có: \(\left(x+4\right)\left(9x^2-1\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(3x-1\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\3x-1=0\\3x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\3x=1\\3x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=\dfrac{1}{3}\\x=-\dfrac{1}{3}\end{matrix}\right.\)
Vậy: \(S=\left\{-4;\dfrac{1}{3};-\dfrac{1}{3}\right\}\)