Các bạn giúp mình ạ 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Ta có: \(A=\dfrac{7}{12}+\dfrac{5}{12}:6-\dfrac{11}{36}\)
\(=\dfrac{7}{12}+\dfrac{5}{72}-\dfrac{11}{36}\)
\(=\dfrac{42}{72}+\dfrac{5}{72}-\dfrac{22}{72}\)
\(=\dfrac{25}{36}\)
b) Ta có: \(B=\left(\dfrac{4}{5}+\dfrac{1}{2}\right):\left(\dfrac{3}{13}-\dfrac{8}{13}\right)\)
\(=\left(\dfrac{8}{10}+\dfrac{5}{10}\right):\dfrac{-5}{13}\)
\(=\dfrac{13}{10}\cdot\dfrac{13}{-5}\)
\(=-\dfrac{169}{50}\)
c) Ta có: \(C=\left(\dfrac{2}{3}-\dfrac{1}{4}+\dfrac{5}{11}\right):\left(\dfrac{5}{12}+1-\dfrac{7}{11}\right)\)
\(=\left(\dfrac{88}{132}-\dfrac{33}{132}+\dfrac{60}{132}\right):\left(\dfrac{55}{132}+\dfrac{132}{132}-\dfrac{84}{132}\right)\)
\(=\dfrac{115}{132}\cdot\dfrac{132}{103}=\dfrac{115}{103}\)

B2"
`a)3/4+1/2-1/4`
`=3/4-1/4+1/2`
`=1/2+1/2=1`
`b)(-2)/3*5/7+(-2)/3*2/7+5/3`
`=(-2)/3*(5/7+2/7)+5/3`
`=-2/3+5/3=1`
`c)(-5)/9+5/9:(1 2/3-2 1/6)`
`=(-5)/9+5/9:(5/3-13/6)`
`=(-5)/9+5/9:(-3)/6`
`=(-5)/9+5/9*(-2)`
`=5/9*(-1-2)`
`=5/9*(-3)=-5/3`
b3:
`a)x*3/6=2/3`
`=>x*1/2=2/3`
`=>x=4/3`
`b)x/150=5/6*(-7)/25`
`=>x/150=(-7)/(6*5)=-7/30`
`=>x/150=(-35)/150`
`=>x=-35`
`c)1/2x+3/5x=3`
`=>11/10x=3`
`=>x=3*10/11=30/11`

Số tiền Nam mua sách: \(320000\times\dfrac{1}{4}=80000\) (đồng)
Số tiền Nam mua vở: \(90000:\dfrac{2}{3}=135000\) (đồng)
Số tiền Nam mua dụng cụ học tập: \(320000-\left(80000+135000\right)=105000\) (đồng)

280 - x.9 = 450
x.9 = 280 - 450
x.9 = -170
x= -170/9

I)1.B
2.B
3.C
4.D
5.C
II)
1.B
2.D
3.B
4.B
5.A
6.B
7.tell....way.
8.C
III)
1.isn't teaching
2.drive
3.has
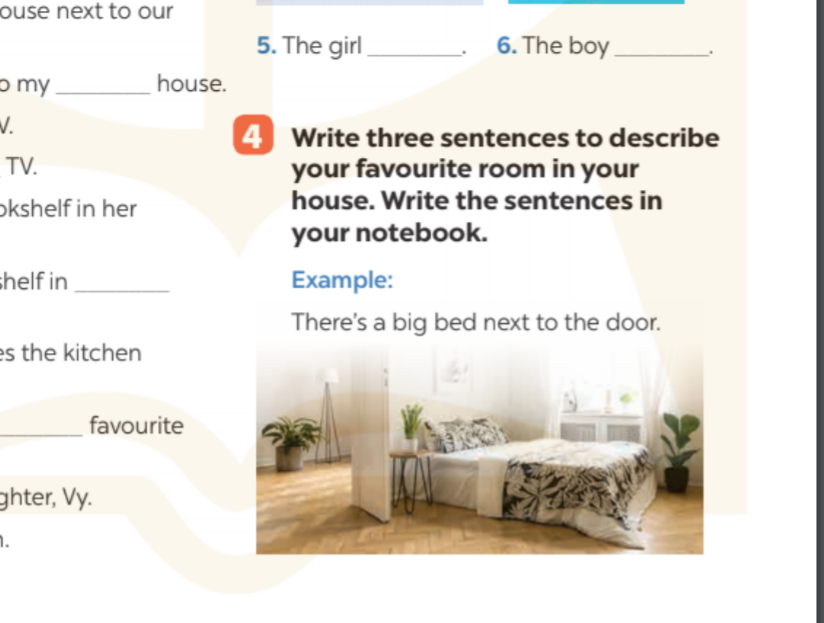 các bạn ơi giúp mình với ạ!!! mình cần gấp lắm ạ. mong các bạn giúp mình. cảm ơn ạ
các bạn ơi giúp mình với ạ!!! mình cần gấp lắm ạ. mong các bạn giúp mình. cảm ơn ạ 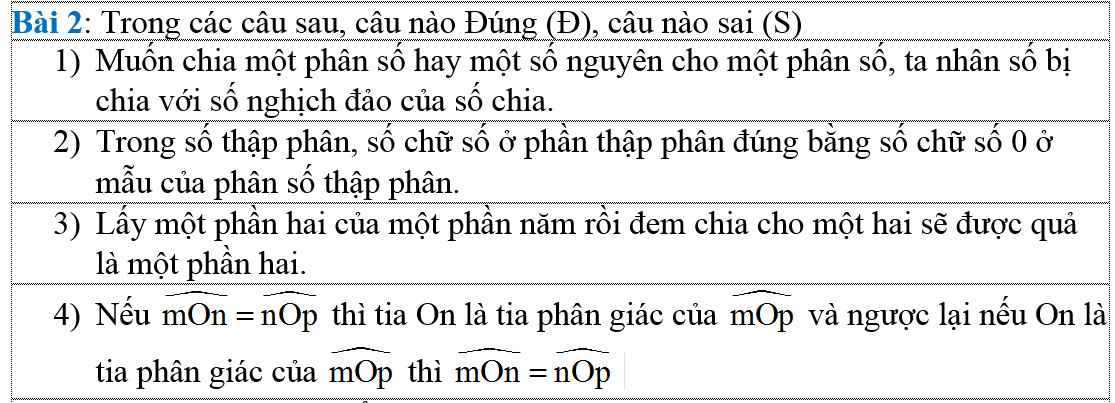

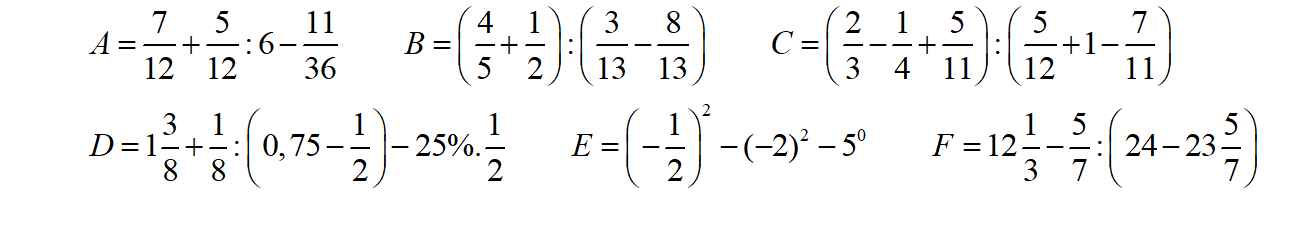


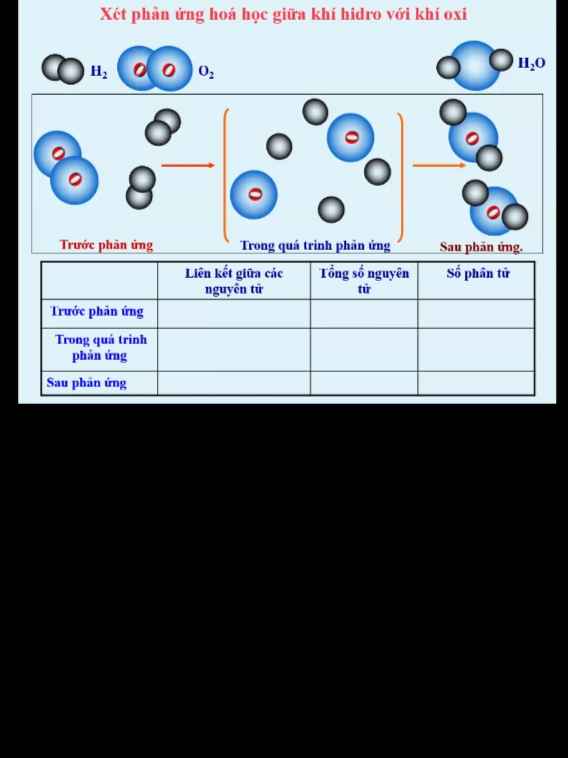

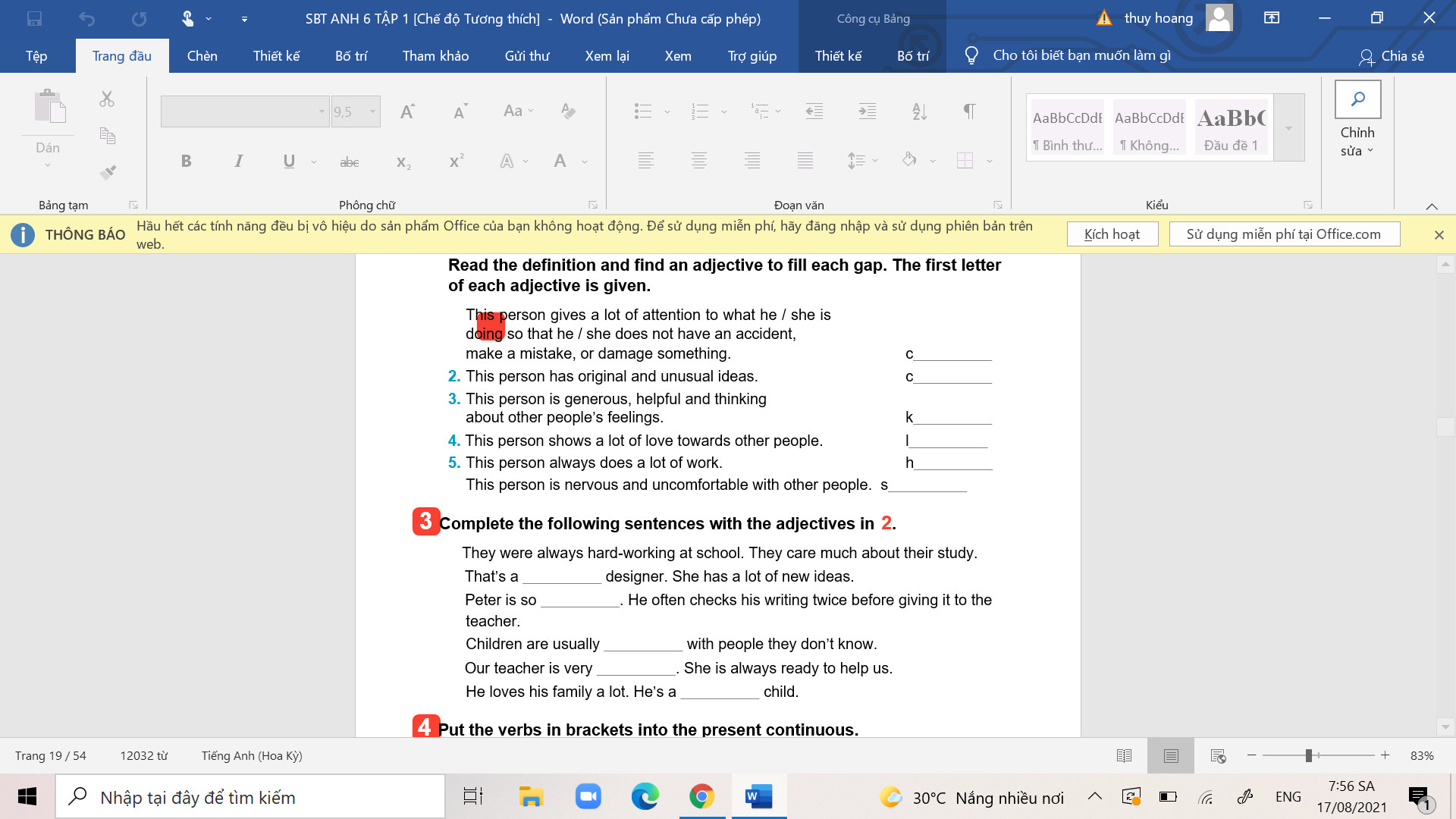 các bn giúp mình bài 2, bài 3.
các bn giúp mình bài 2, bài 3.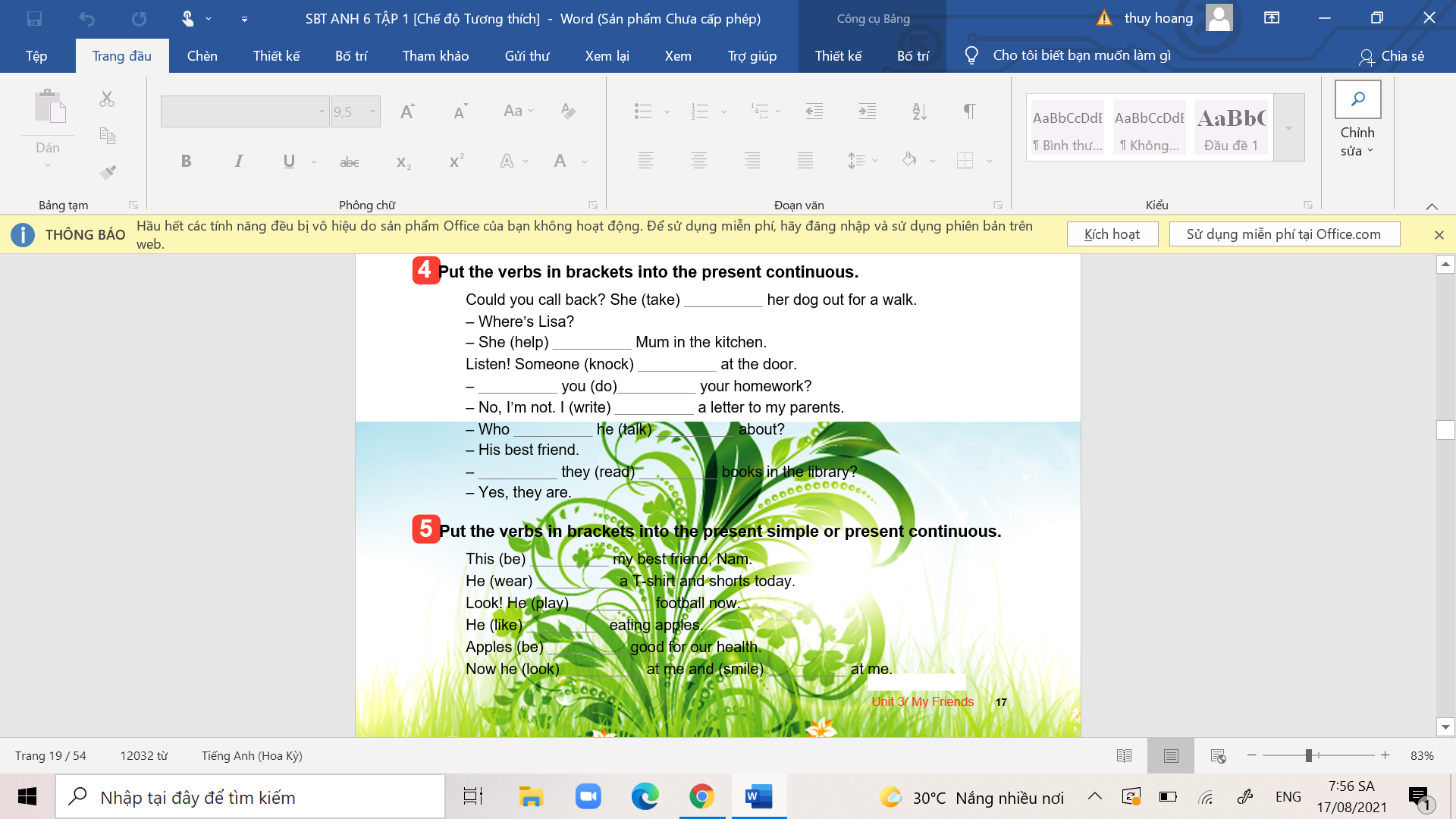 các bn giúp mình bài 4 và bài 5 nhé.
các bn giúp mình bài 4 và bài 5 nhé.
Vì \(CM;CA\) là hai tiếp tuyến cắt nhau của (O) (gt)
\(\Rightarrow OC\) là tia phân giác của \(\widehat{MOA}\) ( t/c hai tiếp tuyến cắt nhau)
\(\Rightarrow\widehat{O_1}=\widehat{O_2}\) (1)
Vì \(DM;DB\) là hai tiếp tiếp tuyến cắt nhau của (O) (gt)
\(\Rightarrow OD\) là tia phân giác của \(\widehat{MOB}\) ( t/c hai tiếp tuyến cắt nhau)
\(\Rightarrow\widehat{O_3}=\widehat{O_4}\) (2)
Lại có: \(\widehat{O_1}+\widehat{O_2}+\widehat{O_3}+\widehat{O_4}=180^0\)(3)
Từ 1; 2 và 3 ta được : \(2\left(\widehat{O_2}+\widehat{O_3}\right)=180^0\)\(\Rightarrow\widehat{COD}=90^0\)
b) Vì \(CM;CA\) là hai tiếp tuyến cắt nhau của (O) (gt)
\(\Rightarrow CM=CA\) (t/c hai \(t^2\) cắt nhau) (4)
Vì \(DM;DB\) là hai tiếp tuyến cắt nhau của (O) (gt)
\(\Rightarrow DM=DB\) (t/c hai \(t^2\) cắt nhau) (5)
Xét \(\Delta COD\) vuông tại O; OM là đường cao:
\(OM^2=CM.MD\) (6)
Từ 4;5 và 6 ta có: \(R^2=AC.BD\) ( vì CM = CA; DM = DB)