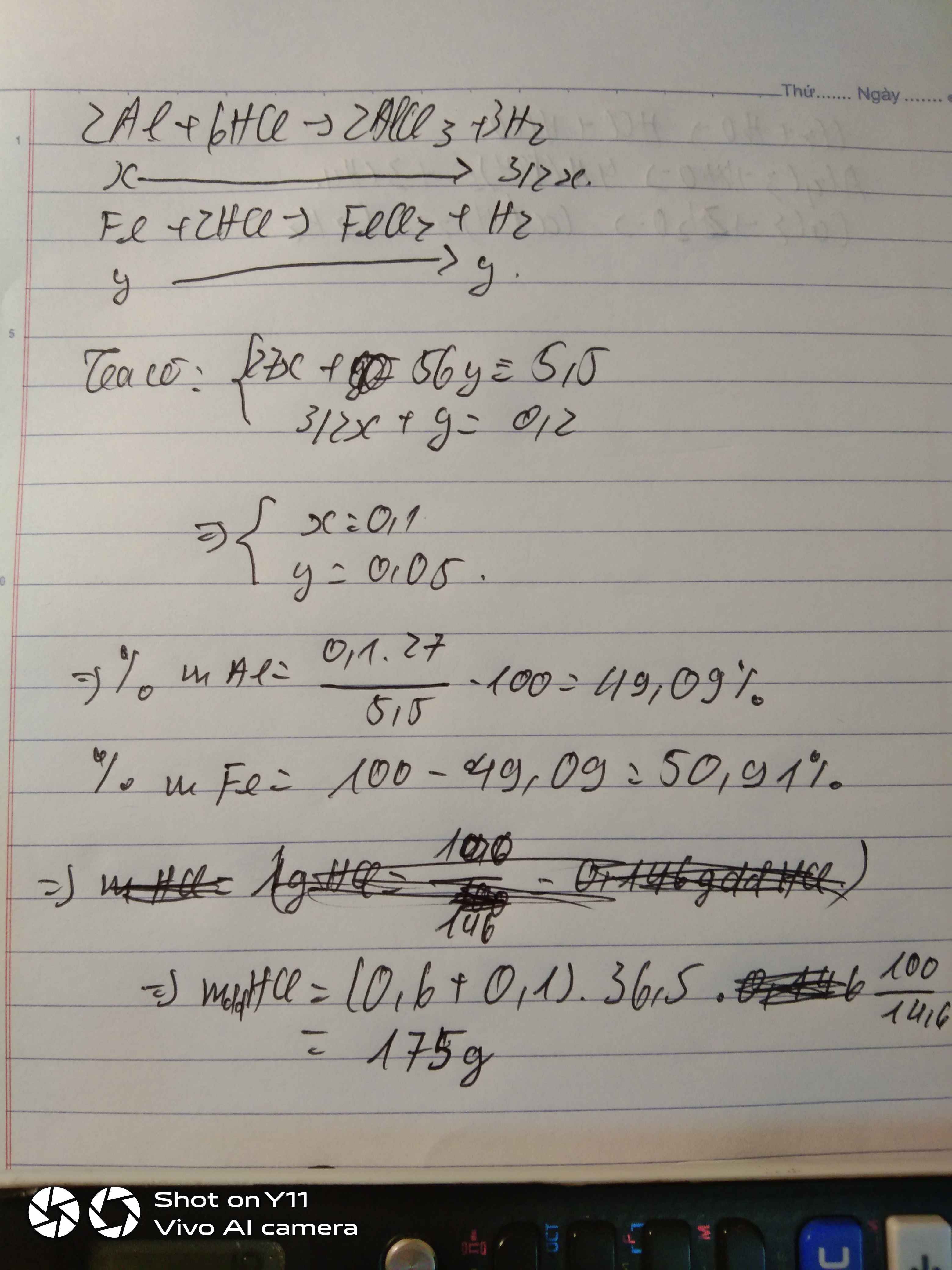Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a, Ta có: 27nAl + 56nFe = 22 (1)
PT: \(2Al+6HCl\rightarrow2AlCl_3+3H_2\)
\(Fe+2HCl\rightarrow FeCl_2+H_2\)
Theo PT: \(n_{H_2}=\dfrac{3}{2}n_{Al}+n_{Fe}=\dfrac{19,832}{24,79}=0,8\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}m_{Al}=0,4\left(mol\right)\\n_{Fe}=0,2\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{Al}=\dfrac{0,4.27}{22}.100\%\approx49,09\%\\\%m_{Fe}\approx50,91\%\end{matrix}\right.\)
b, \(n_{HCl}=2n_{H_2}=1,6\left(mol\right)\)
\(\Rightarrow C_{M_{HCl}}=\dfrac{1,6}{0,5}=3,2\left(M\right)\)

\(n_{Fe}=a\left(mol\right),n_{Mg}=b\left(mol\right)\)
\(m_{hh}=56a+24b=10.16\left(g\right)\)
\(n_{H_2}=\dfrac{5.6}{22.4}=0.25\left(mol\right)\)
\(Fe+2HCl\rightarrow FeCl_2+H_2\)
\(Mg+2HCl\rightarrow MgCl_2+H_2\)
\(n_{H_2}=a+b=0.25\left(mol\right)\left(2\right)\)
\(\left(1\right),\left(2\right):a=0.13,b=0.12\)
\(m_{Fe}=0.13\cdot56=7.28\left(g\right)\)
\(m_{Mg}=0.12\cdot24=2.88\left(g\right)\)
\(n_{HCl}=2\cdot n_{H_2}=2\cdot0.25=0.5\left(mol\right)\)
\(C_{M_{HCl}}=\dfrac{0.5}{0.5}=1\left(M\right)\)

a) PTHH: \(Fe+2HCl\rightarrow FeCl_2+H_2\uparrow\)
a_____2a______a_____a (mol)
\(2Al+6HCl\rightarrow2AlCl_3+3H_2\uparrow\)
b_____3b_______b_____\(\dfrac{3}{2}\)b (mol)
Ta lập HPT: \(\left\{{}\begin{matrix}56a+27b=36,1\\a+\dfrac{3}{2}b=\dfrac{21,28}{22,4}=0,95\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=0,5\\b=0,3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m_{Fe}=0,5\cdot56=28\left(g\right)\\m_{Al}=8,1\left(g\right)\end{matrix}\right.\)
b+c) Theo các PTHH: \(\left\{{}\begin{matrix}n_{HCl}=2a+3b=1,9\left(mol\right)\\n_{FeCl_2}=0,5\left(mol\right)\\n_{AlCl_3}=0,3\left(mol\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}C_{M_{HCl}}=\dfrac{1,9}{0,2}=9,5\left(M\right)\\C_{M_{FeCl_2}}=\dfrac{0,5}{0,2}=2,5\left(M\right)\\C_{M_{AlCl_3}}=\dfrac{0,3}{0,2}=1,5\left(M\right)\end{matrix}\right.\)

a, Ta có: 27nAl + 56nFe = 27,8 (1)
PT: \(2Al+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2\)
\(Fe+H_2SO_4\rightarrow FeSO_4+H_2\)
Theo PT: \(n_{H_2}=\dfrac{3}{2}n_{Al}+n_{Fe}=\dfrac{17,353}{24,79}=0,7\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{Al}=0,2\left(mol\right)\\n_{Fe}=0,4\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{Al}=\dfrac{0,2.27}{27,8}.100\%\approx19,42\%\\\%m_{Fe}\approx80,58\%\end{matrix}\right.\)
b, \(n_{H_2SO_4}=n_{H_2}=0,7\left(mol\right)\Rightarrow C_{M_{H_2SO_4}}=\dfrac{0,7}{0,5}=1,4\left(M\right)\)

Gọi \(\left\{{}\begin{matrix}n_{Al}=x\left(mol\right)\\n_{Fe}=y\left(mol\right)\end{matrix}\right.\)
\(n_{H_2}=\dfrac{4,48}{22,4}=0,2mol\)
\(2Al+6HCl\rightarrow2AlCl_3+3H_2\)
\(Fe+2HCl\rightarrow FeCl_2+H_2\)
Theo pt: \(\Rightarrow\left\{{}\begin{matrix}3x+y=0,2\\27x+56y=5,5\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{19}{470}\\y=\dfrac{37}{470}\end{matrix}\right.\)
\(\%m_{Al}=\dfrac{\dfrac{19}{470}\cdot27}{5,5}\cdot100\%=19,84\%\)
\(\%m_{Fe}=100\%-19,84\%=80,16\%\)

$a)PTHH:2Al+6HCl\to 2AlCl_3+3H_2$
$n_{H_2}=\dfrac{5,04}{22,4}=0,225(mol)$
$\Rightarrow n_{Al}=0,15(mol)$
$\Rightarrow \%m_{Al}=\dfrac{0,15.27}{9,45}.100\%\approx 42,86\%$
$\Rightarrow \%m_{Cu}=100-42,86=57,14\%$
$b)$ Theo PT: $n_{HCl}=2n_{H_2}=0,45(mol)$
$\Rightarrow C_{M_{HCl}}=\dfrac{0,45.110\%}{0,5}=0,99M$