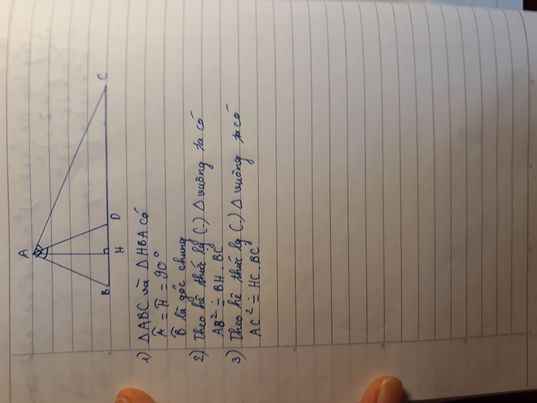
cho tam giác vuông ABC vuông tại A.Kể AH vuông góc với BC.Chứng minh bình phương của AB+bình phương của CH=bình phương của AC+bình phương của BH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
AB
Anh Bùi Thị
3 tháng 2 2021
Đúng(0)
Những câu hỏi liên quan
21 tháng 8 2021
1: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
2: Ta có: ΔABC\(\sim\)ΔHBA
nên \(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)
hay \(AB^2=BH\cdot BC\)
3: Xét ΔACH vuông tại H và ΔBCA vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔACH\(\sim\)ΔBCA
Suy ra: \(\dfrac{CA}{CB}=\dfrac{CH}{CA}\)
hay \(CA^2=CH\cdot CB\)
22 tháng 8 2021
1: Xét ΔABH vuông tại H và ΔCBA vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔABH\(\sim\)ΔCBA
2: Ta có: ΔABH\(\sim\)ΔCBA
nên \(\dfrac{BA}{BC}=\dfrac{BH}{BA}\)
hay \(BA^2=BH\cdot BC\)
25 tháng 8 2021
1: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA
2: Ta có: ΔABC\(\sim\)ΔHBA
nên \(\dfrac{AB}{HB}=\dfrac{CB}{AB}\)
hay \(AB^2=HB\cdot BC\)
25 tháng 6 2016
Bạn ơi đề thiếu hay sao ấy
Phải là :
BD2 - CD2 = ?
Sửa đi mik giải cho
12 tháng 12 2023
c: Sửa đề: D đối xứng với H qua M
Xét ΔAHK có
AN là đường cao
AN là đường trung tuyến
Do đó: ΔAHK cân tại A
Ta có: ΔAHK cân tại A
mà AC là đường cao
nên AC là phân giác của góc HAK
=>\(\widehat{HAK}=2\cdot\widehat{HAC}\)
Xét ΔAHD có
AM là đường cao
AM là đường trung tuyến
Do đó: ΔAHD cân tại A
Ta có: ΔAHD cân tại A
mà AB là đường cao
nên AB là phân giác của góc HAD
=>\(\widehat{HAD}=2\cdot\widehat{HAB}\)
Ta có: \(\widehat{HAK}+\widehat{HAD}=\widehat{DAK}\)
=>\(\widehat{DAK}=2\cdot\widehat{HAB}+2\cdot\widehat{HAC}\)
=>\(\widehat{DAK}=2\left(\widehat{HAC}+\widehat{HAB}\right)=2\cdot\widehat{BAC}=2\cdot90^0=180^0\)
=>D,A,K thẳng hàng
Sửa đề: \(BD^2+CK^2+2\cdot BH\cdot HC\)
Xét ΔBHD có
BM là đường cao
BM là đường trung tuyến
Do đó: ΔBHD cân tại B
=>BH=BD
Xét ΔCKH có
CN là đường cao
CN là đường trung tuyến
Do đó: ΔCKH cân tại C
=>CK=CH
\(BD^2+CK^2+2\cdot BH\cdot HC\)
\(=BH^2+HC^2+2\cdot BH\cdot HC\)
\(=\left(BH+HC\right)^2=BC^2\)
9 tháng 5 2022
a, Xét Δ ABC và Δ CBH
Ta có : \(\widehat{ACB}=\widehat{CHB}=90^o\)
\(\widehat{ABC}=\widehat{CBH}\) (góc chung)
=> Δ ABC ∾ Δ CBH (g.g)
b, Ta có : Δ ABC ∾ Δ CBH (cmt)
=> \(\dfrac{AB}{CB}=\dfrac{BC}{BH}\)
=> \(BC^2=AB.BH\)
9 tháng 5 2022
c,
Ta có : AB = AH + HB
=> AB = 4 + 9
=> AB = 13 (cm)
Ta có : \(BC^2=AB.BH\left(cmt\right)\)
=> \(BC^2=13.9\)
=> \(BC^2=117\)
=> BC = 10,8 (cm)
Xét Δ ABC
Ta có : \(AB^2=AC^2+BC^2\)
=> \(13^2=AC^2+10,8^2\)
=> \(169=AC^2+116,64\)
=> \(169-116,64=AC^2\)
=> \(52,36=AC^2\)
=> AC = 7,2 (cm)
Xét Δ ABC vuông tại C
=> \(S_{\Delta ABC}=\dfrac{AC.BC}{2}\)
=> \(S_{\Delta ABC}=\dfrac{7,2.10,8}{2}\)
=> \(S_{\Delta ABC}=38,88\left(cm^2\right)\)