Cho các hàm số (P) : y = - x2 ; (d) : y = m x – 1
a) Cm :với mọi m (d) luôn cắt (P) tại hai điểm phân biệt
b) Gọi x1, x2 lần lượt là hoành độ các giao điểm của (d) và (P).
Tìm m để x12 x2 – x1x22- x1x2 = 7.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Đồ thị hàm số y = a x 2 (a ≠ 0) là một đường cong đi qua gốc tọa độ và nhận trục tung làm đối xứng.
+ Nếu a > 0 thì đồ thị nằm phía trên trục hoành.
+ Nếu a < 0 thì đồ thị nằm phía dưới trục hoành.
Trong đồ thị các hàm số đã cho; các đồ thị nằm phía dưới trục hoành là”
(1): y = -2 x 2 ; (3): y = - 3 x 2 và (4):y = -10 x 2

Đáp án B
* Hàm số bậc nhất y = ax + b đồng biến khi a > 0 và hàm số này nghịch biến khi a < 0 .
Do đó, hàm số y = 3x đồng biến trên R nên cũng đồng biến khi x < 0 .
Hàm số y = -4x nghịch biến trên R.
* Xét hàm số y = ax2 (a ≠ 0)
Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0.
Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.
Trong hai hàm số y = 3x2 và y = -4x2 chỉ có hàm số y = -4x2 đồng biến khi x < 0
Vậy trong các hàm số đã cho chỉ có hàm số y = 3x và y = -4x2 đồng biến x < 0.

Đáp án C
Đáp án: Hàm số y = x 2 − 2 x − 3 không có đạo hàm tại x = 0
Hàm số y = x 2 − 1 − 4 không có đạo hàm tại x = ± 1. Hàm số y = − x 4 + 2 x 2 − 3 có lim x → ± ∞ = − ∞
Nên bảng biến thiên trên không là bảng biến thiên của 3 hàm số trên. y = x 4 − 2 x 2 − 3
Kiểm tra ta có đó là bảng biến thiên của hàm số: y = x 4 − 2 x 2 − 3

Đáp án C.
Ta có
y = − x 3 + x 2 − 3 x + 1 ⇒ y ' = − 3 x 2 + 2 x − 3 < 0 ; ∀ x ∈ ℝ
suy ra hàm số nghịch biến trên ℝ

+ Xét hàm số y= f(x) = cos3x
TXĐ: D =R
Với mọi x ∈ D , ta có: - x ∈ D và
f( -x) = cos( - 3x) = cos3x = f(x)
Do đó, y= cos 3x là hàm chẵn trên tập xác định của nó.
+ Xét hàm y= g(x)= sin(x2 + 1)
TXĐ: D= R
Với mọi x ∈ D , ta có: - x ∈ D và
g( -x)= sin[ (-x)2 +1]= sin( x2+1)= g(x)
Do đó: y= sin( x2 +1) là hàm chẵn trên R.
+ Xét hàm số y= h( x)= tan2x .
TXĐ: 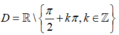
Với mọi x ∈ D , ta có: - x ∈ D và
h( -x)= tan2 (-x)= (- tanx)2 = tan2 x= h(x)
Do đó y= tan2x là hàm số chẵn trên D.
+ Xét hàm số y= t(x)= cotx.
TXĐ: ![]()
Với mọi x ∈ D , ta có: - x ∈ D và t(-x)= cot(-x) = - cotx = - t(x)
Do đó: y= cotx là hàm số lẻ trên D.
Vậy (1); (2); (3) là các hàm số chẵn
Đáp án C

Đáp án A
Xét hàm số y = ax2 (a ≠ 0)
* Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0.
* Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.
Do đó,chỉ có hàm số y = 2x2 đồng biến khi x> 0.

Chọn D.
Ta có tập xác định của hàm số ![]()
Ta có:
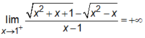
nên x = 1 là đường TCĐ của đồ thị hàm số.
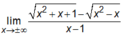
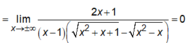
nên đường thẳng y = 0 là TCN của đồ thị hàm số

Đáp án C.
Ta có y ' = 3 x 2 + 4 m − 2 x − 5 ; y ' = 0 ⇔ 3 x 2 + 4 m − 2 x − 5 = 0 (*).
Phương trình (*) có a c < 0 nên luôn có hai nghiệm trái dấu .
Suy ra x 1 = − x 1 ; x 2 = x 2 .
Khi đó x 1 , x 2 là hai điểm cực trị của hàm số.
x 1 − x 2 = − 2 ⇔ − x 1 − x 2 = − 2 ⇔ x 1 + x 2 = 2 ⇔ − 4 m − 2 3 = 2 ⇔ m = 1 2