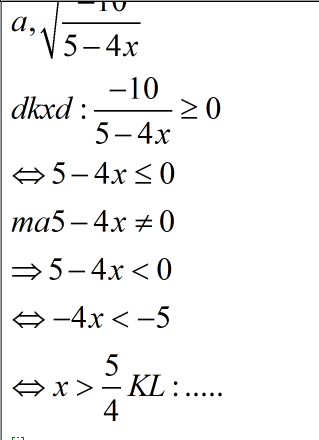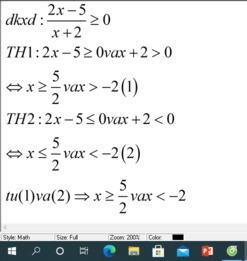Tìm điều kiện xác định của biểu thức : B = \(\sqrt{x^2-3x}\) + \(\sqrt{\dfrac{x-5}{x-1}}\)- \(\sqrt[3]{2x-1}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
18 tháng 12 2020
a/ ĐKXĐ : \(-2x+3\ge0\)
\(\Leftrightarrow x\le\dfrac{3}{2}\)
b/ ĐKXĐ : \(3x+4\ge0\)
\(\Leftrightarrow x\ge-\dfrac{4}{3}\)
c/ Căn thức \(\sqrt{1+x^2}\) luôn được xác định với mọi x
d/ ĐKXĐ : \(-\dfrac{3}{3x+5}\ge0\)
\(\Leftrightarrow3x+5< 0\)
\(\Leftrightarrow x< -\dfrac{5}{3}\)
e/ ĐKXĐ : \(\dfrac{2}{x}\ge0\Leftrightarrow x>0\)
P.s : không chắc lắm á!
13 tháng 8 2023
1: ĐKXĐ: 2-3x>=0
=>x<=2/3
2: ĐKXĐ: -3x^2>=0
=>x^2<=0
=>x=0
3: ĐKXĐ: -2023x^3>=0
=>x^3<=0
=>x<=0
4: ĐKXĐ: -2(x-5)>=0
=>x-5<=0
=>x<=5
5: ĐKXĐ: -5/2-2x>=0
=>2-2x<0
=>2x>2
=>x>1
6: ĐKXĐ: (x^2+1)(3-2x)>=0
=>3-2x>=0
=>-2x>=-3
=>x<=3/2
7: ĐKXĐ: (-x^2-1)(3-x)>=0
=>(x^2+1)(x-3)>=0
=>x-3>=0
=>x>=3
HP
27 tháng 8 2021
a, \(x+1\ge0\Leftrightarrow x\ge-1\)
b, \(1-2x\ge0\Leftrightarrow x\le\dfrac{1}{2}\)
c, \(\left\{{}\begin{matrix}x+1\ge0\\x-2\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x\ge2\end{matrix}\right.\Leftrightarrow x\ge2\)
HP
27 tháng 8 2021
d, \(\left\{{}\begin{matrix}2-3x\ge0\\1-2x\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{2}{3}\\x\le\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow x\le\dfrac{1}{2}\)
e, \(\left\{{}\begin{matrix}\sqrt{3}-2x\ge0\\x-1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{\sqrt{3}}{2}\\x\ne1\end{matrix}\right.\Leftrightarrow x\le\dfrac{\sqrt{3}}{2}\)
14 tháng 8 2021
a: ĐKXĐ: \(-\dfrac{\sqrt{6}}{2}\le x\le\dfrac{\sqrt{6}}{2}\)
b: ĐKXĐ: \(\left[{}\begin{matrix}x\ge1\\x\le-1\end{matrix}\right.\)
c: ĐKXĐ: \(-\sqrt{5}< x< \sqrt{5}\)
d: ĐKXĐ: \(x\le\sqrt[3]{-5}\)
TG
16 tháng 5 2021
a) ĐK: x ≥ 2
\(\sqrt{3x-6}=3\)
\(\Leftrightarrow3x-6=9\)
<=> 3x = 15
<=> x = 5
Vậy:....
b) ĐK: 5x - 16 ≥ 0
<=> 5x ≥ 16
<=> x ≥ 16/5
\(\sqrt{5x-16}=2\)
<=> 5x - 16 = 4
<=> 5x = 20
<=> x = 4
c) ĐK: \(x^2-4x+3\ne0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)\ne0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne1\\x\ne3\end{matrix}\right.\)
16 tháng 5 2021
bình phương hai vế ta được:
a)điều kiện của x:x≥2
3x-6=9 <=> x=5(nhận)
b)ĐK: x≥16/5
5x-16=4 <=>x=4(nhận)
c) ta có: \(\dfrac{2x-3}{\left(x-2\right)^2-1}\)= \(\dfrac{2x-3}{\left(x-3\right)\left(x-1\right)}\)
ĐKXĐ: x≠3 ;x≠1
24 tháng 7 2021
1) ĐKXĐ: \(x\notin\left\{0;1\right\}\)
2) Ta có: \(A=\left(\dfrac{x\sqrt{x}-1}{x-\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}\right):\left(1-\dfrac{3-\sqrt{x}}{\sqrt{x}+1}\right)\)
\(=\dfrac{x+\sqrt{x}+1-\left(x-\sqrt{x}+1\right)}{\sqrt{x}}:\dfrac{\sqrt{x}+1-3+\sqrt{x}}{\sqrt{x}+1}\)
\(=2\cdot\dfrac{\sqrt{x}+1}{2\sqrt{x}-2}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
11 tháng 8 2021
a: ĐKXĐ: \(\dfrac{x-1}{5-x}\ge0\)
\(\Leftrightarrow\dfrac{x-1}{x-5}\le0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-1\ge0\\x-5< 0\end{matrix}\right.\Leftrightarrow1\le x< 5\)
b: ĐKXĐ: \(\left[{}\begin{matrix}x>3\\x< 2\end{matrix}\right.\)
N
2
7 tháng 2 2022
a) \(\sqrt{3x-4}\) xác định \(\Leftrightarrow3x-4\ge0\Leftrightarrow3x\ge4\Leftrightarrow x\ge\dfrac{4}{3}\)
b) \(\dfrac{1}{\sqrt{x-4}}\) xác định \(\Leftrightarrow x-4>0\Leftrightarrow x>4\)