cho tam giác ABC nhọn nội tiếp đường tròn tâm O đường kính AD (AB < AD ) gọi H là trực tâm tam giác ABC , M là điểm chính gjữa cung nhỏ BC . Chứng minh
a) AM la phan giac goc HAD
b) tứ giác BHCD là hình gì
c ) goi I la trung diem BC , K la trung diem AH , tia phan giâc ACH cat tia phan giac ABH tai n , chung minh 3 diem K, N , I thang hang

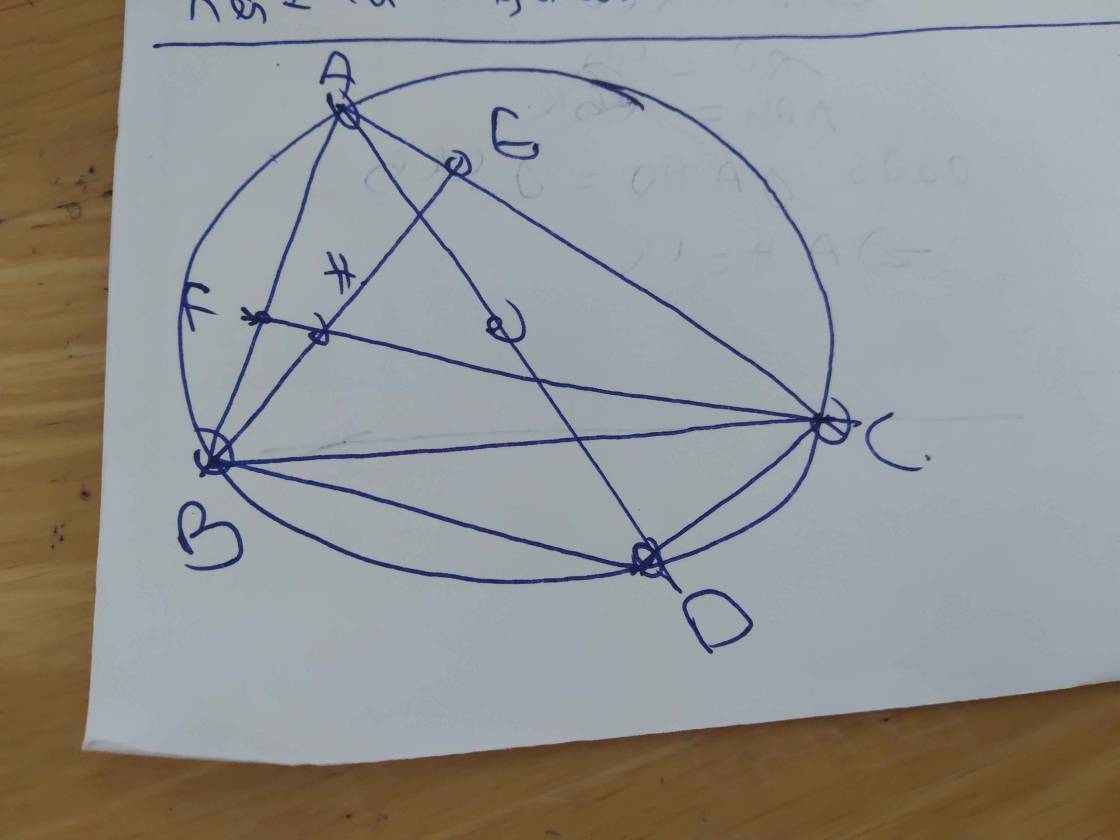


M để làm gì vậy bn?
BHCD là hình bình hành
(*mình kí hiệu '^' là góc nhé!)
a)nối C với D. Ta có ^ACD=90° (nt chắn nửa đg tròn) => ^CAD+^CDA =90° (1). Goi K là chân đường cao hạ từ A xuống BC, ta có ^AKB=90° => ^KAB+^KBA=90° (2). Ta có ^KBA=^CDA=1/2 sđ cung AC nhỏ (3). Từ (1),(2) va (3) => ^KAB=^CAD (4). Điểm M nằm chinh giữa cung BC nhỏ => ^BAM=^CAM (5). Ta có ^BAM=^KAM+^KAB (6) ;ta có ^CAM=^DAM+^CAD (7). Từ (4),(5),(6) và (7) =>^KAM=^DAM => AM là phân giác ^HAD.
b)Gọi E là chân đường cao hạ từ B xuống AC, F là chân đường cao hạ từ C xuống AB. Ta có BE vuông góc AC, DC vuông góc AC (^ACD=90°) => DC//BF <=>DC//BH (8).Tương tự ta có DB//CH (9) ,từ (8) và (9) => BHCD là hình bình hành.