Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


=a^3+b^3+3a^2b+3ab^2-a^3+3a^2b-3ab^2+b^3-2b^3
=6a^2b

(a + b)3 – (a – b)3 – 2b3
= (a3 + 3a2b + 3ab2 + b3) – (a3 – 3a2b + 3ab2 – b3) – 2b3 (Áp dụng HĐT (4) và (5))
= a3 + 3a2b + 3ab2 + b3 – a3 + 3a2b – 3ab2 + b3 – 2b3
= (a3 – a3) + (3a2b + 3a2b) + (3ab2 – 3ab2) + (b3 + b3 – 2b3)
= 6a2b

Áp dụng hằng đẳng thức dưới dạng
\(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)\)
\(\left(a+b+c\right)^3+\left(a-b-c\right)^3=\left(2a\right)^3-3\left(a+b+c\right)\left(a-b-c\right).2a\)
\(\left(b-c-a\right)^3+\left(c-a-b\right)^3=\left(-2a\right)^3-3\left(b-c-a\right)\left(c-a-b\right).\left(-2a\right)\)
\(\Rightarrow\left(a+b+c\right)^3+\left(a-b-c\right)^3+\left(b-c-a\right)^3+\left(c-a-b\right)^3\)
\(=\left(2\right)^3+\left(-2a\right)^3-6a\left[a+\left(b+c\right)\right]\left[a-\left(b+c\right)\right]+6a\left[-a+\left(b-c\right)\right]\left[-a-\left(b-c\right)\right]\)
\(=-6a\left\{a^2-\left(b+c\right)^2-\left[\left(-a\right)^2-\left(b-c\right)^2\right]\right\}\)
\(=-6a\left\{a^2-a^2+\left(b-c\right)^2-\left(b+c\right)^2\right\}\)
\(=-6a\left[b-c+b+c\right]\left[b-c-\left(b+c\right)\right]=-6a.2b.\left(-2c\right)\)
\(=24abc\)

=\(\dfrac{\left(a-b\right)\left(\sqrt{a}-\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}-\dfrac{\sqrt{a^3}-\sqrt{b^3}}{a-b}\)
=\(\dfrac{\sqrt{a^3}-\sqrt{b^3}}{a-b}-\dfrac{\sqrt{a^3}-\sqrt{b^3}}{a-b}\)
=\(0\)

a,Đặt a+b-c=x, c+a-b=y, b+c-a=z
=>x+y+z=a+b-c+c+a-b+b+c-a=a+b+c
Ta có hằng đẳng thức:
(x+y+z)^3-3x-3y-3z=3(x+y)(x+z)(y+z)
=>(a+b+c)^3-(b+c-a)^3-(a+c-b)^3-(a+b-c)^3=(x+y+z)^3-x^3-y^3-z^3
=3(x+y)(x+z)(y+z)
=3(a+b-c+c+a-b)(c+a-b+b+c-a)(b+c-a+a+b-c)
=3.2a.2b.2c
=24abc

Đặt \(x=a+b;y=b+c;z=c+a\) ta có:
\(x^3+y^3+z^3-3xyz\)
\(=\left(x+y\right)^3-3xy\left(x-y\right)+z^3-3xyz\)
\(=\left[\left(x+y\right)^3+z^3\right]-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)^3-3z\left(x+y\right)\left(x+y+z\right)-3xy\left(x-y-z\right)\)
\(=\left(x+y+z\right)\left[\left(x+y+z\right)^2-3z\left(x+y\right)-3xy\right]\)
\(=\left(x+y+z\right)\left(x^2+y^2+z^2+2xy+2xz+2yz-3xz-3yz-3xy\right)\)
\(=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-yx\right)\)
Thay vào ta có:\(\left(a+b+b+c+c+a\right)\left[\left(a+b\right)^2+\left(b+c\right)^2+\left(c+a\right)^2-\left(a+b\right)\left(b+c\right)-\left(b+c\right)\left(c+a\right)-\left(c+a\right)\left(a+b\right)\right]\)
\(=\left(2a+2b+2c\right)\left(a^2-ab-ac+b^2-bc+c^2\right)\)
\(=2\left(a+b+c\right)\left(a^2-ab-ac+b^2-bc+c^2\right)\)

Câu hỏi của Nhàn Nguyễn - Toán lớp 8 - Học toán với OnlineMath
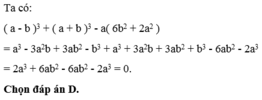
Rút gọn biểu thức: (a+b)\(^3\) – (a–b)\(^3\)
Ta có: \(\left(a+b\right)^3-\left(a-b\right)^3\)
= \(a^3+3a^2b+3ab^2+b^3-a^3-3a^2b+3ab^2-b^3\)
= \(6ab^2\)
(a+b)3-(a-b)3 = a3+3a2b+3ab2+b3-a3+3a2b-3ab2+b3
=6a2b+2b3 =2b(3a2 +b2)