cho hình thoi cạnh 3cm. tỏng các bình phương của 2 đường chéo bằng bao nhiu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GB
4
28 tháng 3 2022
câu 2
Bài giải:
Chu vi hình bình hành là:
(6+5)x2= 22(cm)
Chiều cao hình bình hành là:
6x\(\dfrac{2}{3}\)= 4(cm)
Diện tích hình bình hành là:
6x4= 24(cm2)
Đáp số: 22cm
24cm2
28 tháng 3 2022
câu 3
bài giải:
Đường chéo thứ hai của mảnh vườn hình thoi dài là:
96x\(\dfrac{3}{8}\)= 36(m)
Diện tích mảnh vườn hình thoi dài là:
(96x36):2= 1728(m2)
Đáp số: 1728 m2
PT
1
CM
23 tháng 11 2017
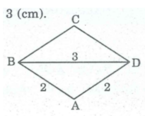
*Cách dựng:
- Dựng ∆ ABD biết AB = AD = 2(cm), BD = 3(cm).
- Trên nửa mặt phẳng bờ BD không chứa điểm A. Từ B dựng tia Bx // AD, từ D dựng tia DY // AB, chúng cắt nhau tại C.
Ta có hình thoi ABCD cần dựng
*Chứng minh:
Vì AB // CD và AD // BC nên tứ giác ABCD là hình bình hành
AB = AD = 2cm. Vậy tứ giác ABCD là hình thoi.
Lại có: BD = 3cm
Hình thoi dựng được thỏa mãn điều kiện bài toán.
CM
14 tháng 8 2017
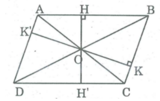
Gọi O là giao điểm hai đường chéo của hình bình hành ABCD, khoảng cách từ O đến cạnh AB là OH = 2cm , đến cạnh BC là OK = 3cm
* Kéo dài OH cắt cạnh CD tại H'.
Ta có OH ⊥ BC
⇒ OH' ⊥ CD và OH' = 2cm
Suy ra HH' bằng đường cao của hình bình hành.
S
A
B
C
D
= HH'.AB ⇒ 
* Kéo dài OK cắt AD tại K'.
Ta có: OK ⊥ BC ⇒ OK' ⊥ CD và OK' = 3 (cm)
Suy ra KK' là đường cao của hình bình hành.
S
A
B
C
D
= KK'.AB ⇒ 
Chu vi của hình bình hành ABCD là (6 + 4).2 = 20 (cm).