Cho các số x, y thỏa mãn:
2x+3y=13. Tính GTNN của Q= x2 +y2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VM
2
AH
Akai Haruma
Giáo viên
19 tháng 6 2021
Lời giải:
Áp dụng BĐT AM-GM:
$x^2+y^2\geq 2\sqrt{x^2y^2}=2|xy|\geq 2xy$
$\Rightarrow 3(x^2+y^2)\geq 6xy$
$x^2+9\geq 2\sqrt{9x^2}=2|3x|\geq 6x$
$y^2+9\geq 2\sqrt{9y^2}=2|3y|\geq 6y$
Cộng theo vế các BĐT trên:
$4(x^2+y^2)+18\geq 6(xy+x+y)=90$
$\Rightarrow x^2+y^2=18$
Vậy $A_{\min}=18$ khi $(x,y)=(3,3)$
AH
Akai Haruma
Giáo viên
20 tháng 6 2021
Sầu Riêng: của em nếu $x,y$ dương thì đúng. Còn trong bài $x,y$ thực thì đến đoạn $(x+y+2)^2\geq 64$ thì không khẳng định $x+y\geq 6$ được nha.
CM
16 tháng 8 2017
Đáp án A.
Ta có x2 + 9y2 = 6xy <=> (x – 3y)2 = 0 <=> x = 3y.
⇒ M = 1 + log 12 x + log 12 y 2 . log 12 6 y = log 12 12 + log 12 3 y 2 log 12 36 y 2
= log 12 36 y 2 log 12 36 y 2 = 1 .
KR
7 tháng 5 2018
Áp dụng Bunyakovsky, ta có :
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)
=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)
=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)
Mấy cái kia tương tự
CM
19 tháng 9 2018
Đáp án C.
Phương pháp giải: Dựa vào giả thiết, đánh giá đưa về tổng các bình phương, từ biểu thức P đưa về hạng tử trong tổng bình phương và áp dụng bất đẳng thức Bunhiacopxki tìm giá trị lớn nhất.
Lời giải:
Vì x2 + y2 > 1 suy ra log x 2 + y 2 f ( x ) là hàm số đồng biến trên tập xác định
Khi đó 
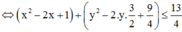
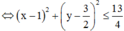
Xét biểu thức P, ta có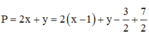 
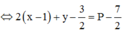
Áp dụng BĐT Bunhiacopxki, có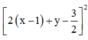 
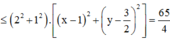
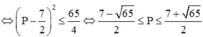
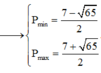
mk copy trên trang này
https://lazi.vn/edu/exercise/311935/cho-cac-so-thoa-man-2x-3y-13-tim-gia-tri-nho-nhat-cua-q
\(2x+3y=13\Rightarrow y=\dfrac{13-2x}{3}\)
\(Q=x^2+\left(\dfrac{13-2x}{3}\right)^2=\dfrac{13}{9}x^2-\dfrac{52}{9}x+\dfrac{169}{9}\)
\(Q=\dfrac{13}{9}\left(x-2\right)^2+13\ge13\)
\(Q_{min}=13\) khi \(\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)