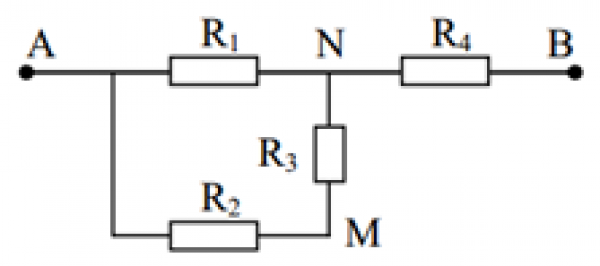
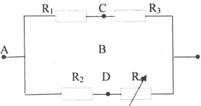
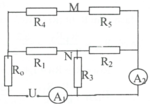
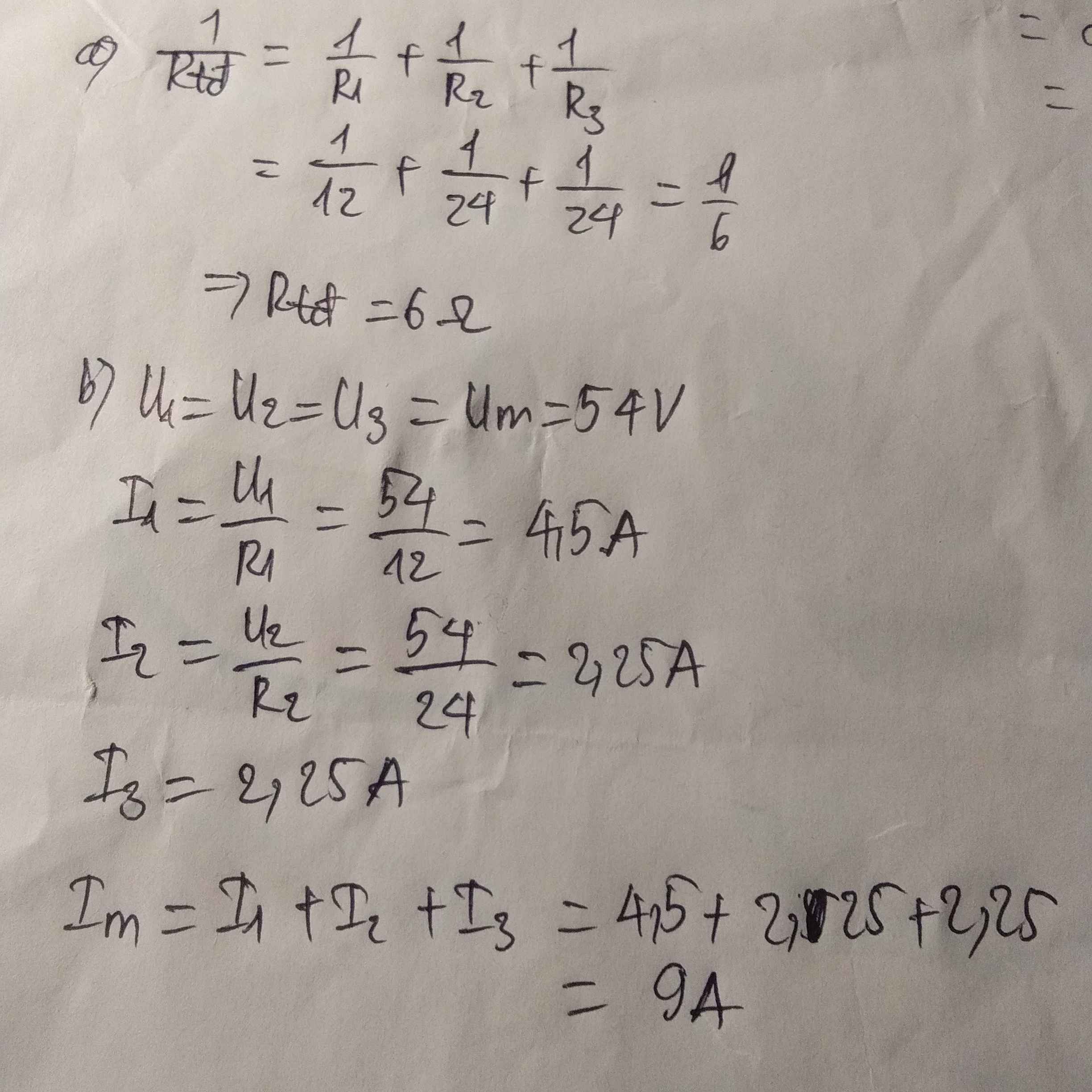cho mạch điện như hình 2 .Hiệu điện thế đặt vào hai đầu A,B có giá trị U không đổi .Biết R1=R2=R3=R4=R0. 1. Mắc vào hai điểm B, D 1 ampe kế lí tưởng. Hãy tính: a, Điện trở tương đương của đoạn mạch AB...

TB

tran bao trung

9 tháng 12 2020 - olm

cho mạch điện như hình 2 .Hiệu điện thế đặt vào hai đầu A,B có giá trị U không đổi .Biết R1=R2=R3=R4=R0. 1. Mắc vào hai điểm B, D 1 ampe kế lí tưởng. Hãy tính: a, Điện trở tương đương của đoạn mạch AB theo R0. b, Số chỉ của ampe kế theo U và R0 . 2.Tháo ampe kế ra khỏi B,D.DÙng vôn kế có điện trở R0 lần lượt đo hiẹu điện thế giữa hai đầu các điện trở R1 và R2 thì số chỉ vôn kế...

Đọc tiếp

#Vật lý lớp 9

0

NQ

Nguyễn quốc việt

1 tháng 11 2021

Câu 1: Có ba điện trở R1= R2 = 60 , R3 = 120 mắc như hình vẽ, hiệu điện thế đặt vào hai đầu đoạn mạch là 120V. a) Tính điện trở tương đương của đoạn mạch? b) Tính cường độ dòng điện trong mạch và qua các điện trở? Và hiệu điện thế đặt vào hai đầu các điện trở?

#Vật lý lớp 9

2

N

nthv_.

1 tháng 11 2021

a. \(R=R1+\left(\dfrac{R2.R3}{R2+R3}\right)=60+\left(\dfrac{60.120}{60+120}\right)=100\left(\Omega\right)\)

b. \(I=I1=I23=U:R=120:100=1,2A\left(R1ntR23\right)\)

\(U1=I1.R1=1,2.60=72V\)

\(U2=U3=U23=U-U1=120-72=48\left(V\right)\)(R1//R2)

\(\left[{}\begin{matrix}I2=U2:R2=48:60=0,8A\\I3=U3:R3=48:120=0,4A\end{matrix}\right.\)

Đúng(1)

C

creeper

1 tháng 11 2021

1589886725-cach-giai-bai-tap-dinh-luat-om-cho-doan-mach-hon-hop-19png.png

Đúng(0)

HD

Hoàng Đức Long

16 tháng 8 2018

Cho mạch điện như hình vẽ. Biết R 1 = 4 Ω , R 2 = R 3 = 6 Ω , R 4 là biến trở. Đặt vào hai đầu mạch điện một hiệu điện thế U A B = 33 ( V ) . 1. Mắc vào CD một ampe kế có điện trở rất nhỏ không đáng kể và điều chỉnh R 4 để cho R 4 = 14 Ω ....

Đọc tiếp

#Vật lý lớp 11

1

VT

Vũ Thành Nam

16 tháng 8 2018

Đúng(0)

H

Haodeptrai

11 tháng 10 2023

Một đoạn mạch gồm 3 điện trở mắc nối tiếp R1 = 3 , R2 = 2,5 , R3 = 4,5  được nối vào hai cực của một nguồn điện . Ampe kế chỉ 0,6 A a. Tính điện trở tương đương của đoạn mạch 1 điểm b. Tính hiệu điện thế hai đầu mỗi điện trở và ở hai đầu đoạn mạch 1 điểm

#Vật lý lớp 9

2

H

Haodeptrai

11 tháng 10 2023

Cứu em với sáng mai kiểm tra rồi huhu

Đúng(0)

DK

Đăng Khoa

11 tháng 10 2023

a) Ta có R\(_1\) nt R\(_2\) nt R\(_3\)

R\(_{tđ}\) = R\(_1\) + R\(_2\) + R\(_3\) = 3 + 2.5 + 4.5 = 10 ( ôm)

b) Ta có: I\(_1\) = I\(_2\) = I\(_3\) ( ĐM nối tiếp)

U\(_1\)= I*R= 0.6 * 3 = 1.8 (V)

U\(_2\)= I *R = 0.6 * 2.5 = 1.5 (V)

U\(_3\)= I* R = 0.6 * 4.5= 2.7 (V)

U= U\(_3\) + U\(_1\)\(\) + U\(_2\)= 2.7+ 1.8 + 1.5 = 6 (V)

Đúng(1)

HH

Hà Huệ

21 tháng 12 2020

Cho mạch điện như hình vẽ biết R1 = 3 ôm R2 = 6 ôm ampe kế có điện trở không đáng kể hiệu điện thế giữa hai đầu đoạn mạch Uab = 18 V không đổi a Tính điểm Điện trở tương đương của đoạn mạch b tìm số chỉ của ampe kế

#Vật lý lớp 9

0

NL

Nguyễn Lê Nhất Bình

6 tháng 10 2021

Một đoann mạch gồm 3 điện trở R1=R2=20 ôm song song và R3=30 ôm mắc nối tiếp với 2 điện trở trên. Đặt vào hai đầu mạch một hiệu điện thế không đổi U=18V. Tính a. Tính điện trở tương đương của đoạn mạch trên b. Hiệu điện thế giữa hai đầu điện trở.

#Vật lý lớp 9

1

N

nthv_.

6 tháng 10 2021

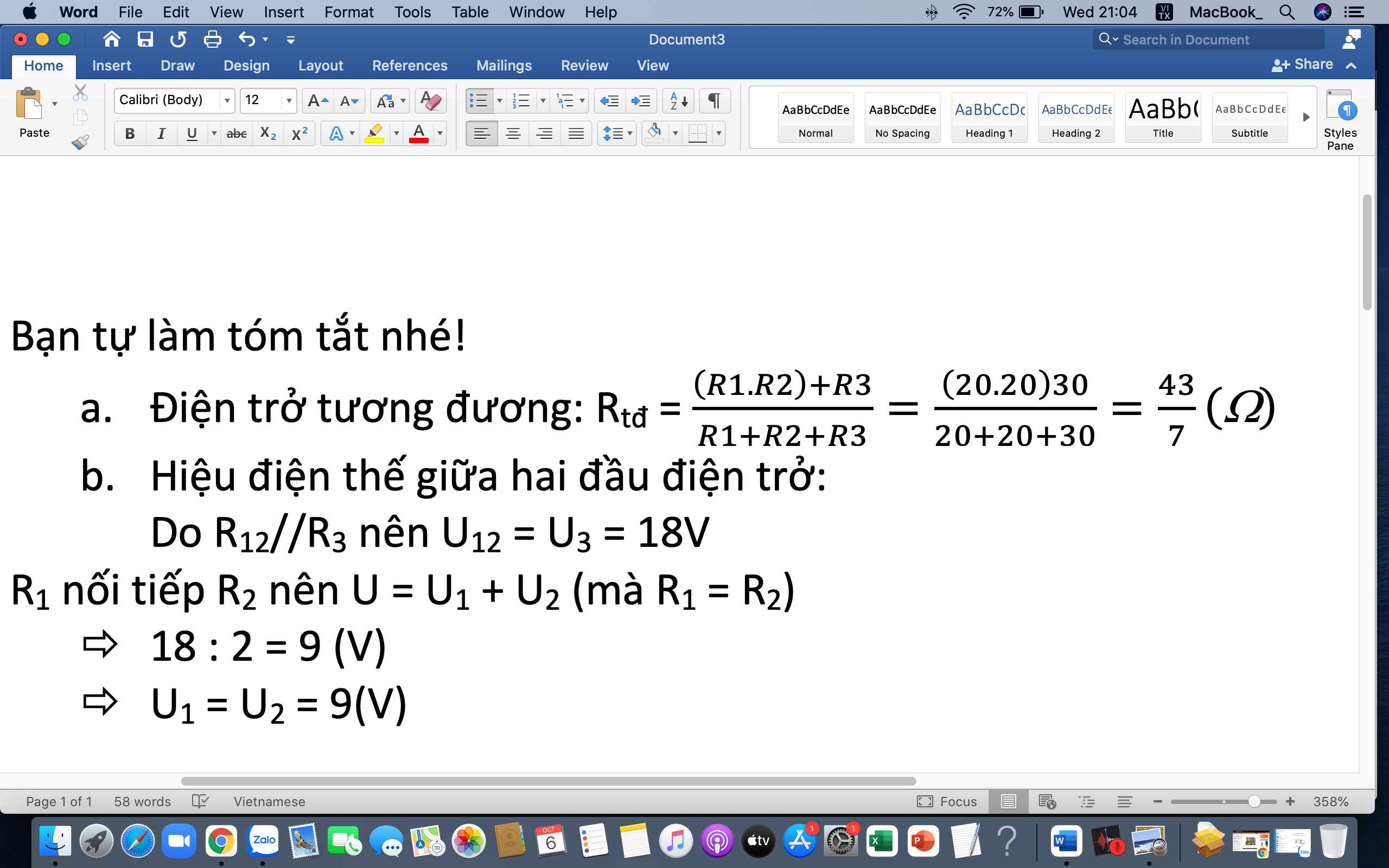
undefined

Đúng(2)

NQ

Nguyễn Quốc Việt

31 tháng 10 2021

Câu 1: Cho mạch điện gồm ba điện trở R1 =12, R2 = R3 = 24, mắc song song với nhau. a) Tính điện trở tương đương của đoạn mạch? b) Đặt vào hai đầu đoạn mạch một hiệu điện thế không đổi U = 54V. Tính dòng điện qua các điện trở và dòng điện trong mạch chính?

#Vật lý lớp 9

2

NT

nguyễn thị hương giang

31 tháng 10 2021

undefined

Đúng(0)

N

nthv_.

31 tháng 10 2021

a. \(\dfrac{1}{R}=\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}=\dfrac{1}{12}+\left(\dfrac{1}{24}\right)^2=\dfrac{1}{6}\Rightarrow R=6\left(\Omega\right)\)

b. \(U=U1=U2=U3=54V\)(R1//R2//R3)

\(\left[{}\begin{matrix}I=U:R=54:6=9A\\I1=U1:R1=54:12=4,5A\\I2=U2:R2=54:24=2,25A\\I3=U3:R3=54:24=2,25A\end{matrix}\right.\)

Đúng(1)

TT

Trần Thanh Huyền

1 tháng 1 2022

Ba điện trở R1 = 10Ω, R2 = R3 =20Ω được mắc song song với nhau vào giữa hai điểm A và B có hiệu điện thế là U.a. Tính đoeẹn trở tương đương của đoạn mạch b. Biết cường độ dòng điện qua R1 có giá trị là 2,4A. Tìm hiệu điện thế U giữa hai đầu đoạn mạch và cường độ dòng điện chạy qua mạch chính và các mạch rẽ còn...

Đọc tiếp

#Vật lý lớp 9

1

LL

Lấp La Lấp Lánh

1 tháng 1 2022

Điện trở tương đương của đoạn mạch là:

\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}=\dfrac{1}{10}+\dfrac{1}{20}+\dfrac{1}{20}=\dfrac{1}{5}\Rightarrow R_{tđ}=5\left(\Omega\right)\)

Do mắc song song nên \(U=U_1=U_2=I_1.R_1=2,4.10=24\left(V\right)\)

Cường độ dòng điện chạy qua mạch chính và các mạch rẽ còn lại:

\(\left\{{}\begin{matrix}I=\dfrac{U}{R_{tđ}}=\dfrac{24}{5}=4,8\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{24}{20}=1,2\left(A\right)\\I_3=\dfrac{U_3}{R_3}=\dfrac{24}{20}=1,2\left(A\right)\end{matrix}\right.\)

Đúng(1)

NH

Nguyen Huynh

2 tháng 1 2022

undefined