Giải phương trình f′(x) = g(x), biết rằng f ( x ) = 1 2 sin 2 x + 5 cos x , g ( x ) = 3 sin 2 x + 3 1 + tan 2 x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) f'(x) = - 3sinx + 4cosx + 5. Do đó
f'(x) = 0 <=> - 3sinx + 4cosx + 5 = 0 <=> 3sinx - 4cosx = 5
<=> sinx -
cosx = 1. (1)
Đặt cos φ = , (φ ∈
) => sin φ =
, ta có:
(1) <=> sinx.cos φ - cosx.sin φ = 1 <=> sin(x - φ) = 1
<=> x - φ = + k2π <=> x = φ +
+ k2π, k ∈ Z.
b) f'(x) = - cos(π + x) - sin = cosx + sin
.
f'(x) = 0 <=> cosx + sin = 0 <=> sin
= - cosx <=> sin
= sin
<=> =
+ k2π hoặc
= π - x +
+ k2π
<=> x = π - k4π hoặc x = π + k, (k ∈ Z).

a) \(f'(x)=g(x)\)
\(\Leftrightarrow 6\sin ^22x\cos 2x=4\cos 2x-5\sin 4x\)
\(\Leftrightarrow 3\sin ^22x\cos 2x=2\cos 2x-5\sin 2x\cos 2x\)
\(\Leftrightarrow \cos 2x(3\sin ^22x-2+5\sin 2x)=0\)
\(\Leftrightarrow \cos 2x(3\sin 2x-1)(\sin 2x+2)=0\)
\(\Rightarrow \left[\begin{matrix} \cos 2x=0\\ \sin 2x=\frac{1}{3}\\ \sin 2x=-2\end{matrix}\right.\)
Với \(\cos 2x=0\Rightarrow x=\frac{\pm \pi}{4}+k\pi (k\in\mathbb{Z})\)
Với \(\sin 2x=\frac{1}{3}\Rightarrow x=\frac{1}{2}\arcsin \frac{1}{3}+k\pi \) hoặc \(x=\pi -\frac{1}{2}\arcsin \frac{1}{3}+k\pi\)
Với \(\sin 2x=-2\) thì loại vì $\sin 2x\in [-1;1]$
b) \(f'(x)=g(x)\)
\(\Leftrightarrow -x^2\sin x+4x\cos ^2\frac{x}{2}=x-x^2\sin x\)
\(\Leftrightarrow 4x\cos ^2\frac{x}{2}=x\)
\(\Leftrightarrow x(4\cos ^2\frac{x}{2}-1)=0\)
\(\Rightarrow \left[\begin{matrix} x=0\\ \cos ^2\frac{x}{2}=\frac{1}{4}\rightarrow \cos \frac{x}{2}=\pm \frac{1}{2}\end{matrix}\right.\)
Với \(\cos \frac{x}{2}=\frac{1}{2}\Rightarrow x=\pm \frac{2\pi}{3}+4k\pi \) với $k$ nguyên.
Với \(\cos \frac{x}{2}=\frac{-1}{2}\Rightarrow x=\frac{-4\pi}{3}+4k\pi \) với $k$ nguyên.

\(a,f'\left(x\right)=3x^2-6x\\ f'\left(x\right)\le0\Leftrightarrow3x^2-6x\le0\\ \Leftrightarrow3x\left(x-2\right)\le0\Leftrightarrow0\le x\le2\)
Lời giải:
a. $f'(x)\leq 0$
$\Leftrightarrow 3x^2-6x\leq 0$
$\Leftrightarrow x(x-2)\leq 0$
$\Leftrightarrow 0\leq x\leq 2$
b.
$f'(x)=x^2-3x+2=0$
$\Leftrightarrow 3x^2-6x=x^2-3x+2=0$
$\Leftrightarrow 3x(x-2)=(x-1)(x-2)=0$
$\Leftrightarrow x-2=0$
$\Leftrightarrow x=2$
c.
$g(x)=f(1-2x)+x^2-x+2022$
$g'(x)=(1-2x)'f(1-2x)'_{1-2x}+2x-1$
$=-2[3(1-2x)^2-6(1-2x)]+2x-1$
$=-24x^2+2x+5$
$g'(x)\geq 0$
$\Leftrightarrow -24x^2+2x+5\geq 0$
$\Leftrightarrow (5-12x)(2x-1)\geq 0$
$\Leftrightarrow \frac{-5}{12}\leq x\leq \frac{1}{2}$
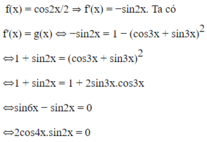
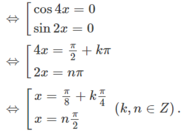
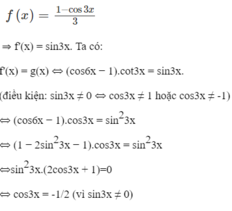
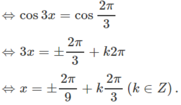
f(x) = sin2x/2 + 5cosx ⇒ f′(x) = cos2x − 5sinx. Ta có
f′(x) = g(x)