Cho 2 điểm A, B phân biệt, không cùng thuộc đường thẳng xy. Xác định vị trí của 1 điểm \(N\in xy\) sao cho: NA+NB đạt giá trị nhỏ nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mọi người làm nhanh jup mik nhé, ai có đáp án sẽ k luôn. Kamsa =)

Bày này chỉ có đạt giá trị lớn nhất thôi nhé ! Bạn xem lại đề !
Lời giải :
Gọi \(M\) là trung điểm của \(BC.\) \(\Rightarrow AM\) không đổi.
Kẻ \(KM\perp DE\)
Khi đó tứ giác \(BDEC\) là hình thang. \(\left(BD//KM//EC\right)\)
Xét hình thang \(BDCE\) có : \(M\) là trung điểm của \(BC,\) \(BD//KM//EC\) ( cmt )
\(\Rightarrow K\) là trung điểm của \(DE\)
\(\Rightarrow KM\) là đường trung bình của hình thang \(BDEC\)
\(\Rightarrow BD+EC=2.KM\)
Mặt khác ta có : \(KM\le AM\) nên \(BD+EC\le2AM\)
Dấu "=" xảy ra \(\Leftrightarrow xy\perp AM\)
Vậy \(BD+CE\) đạt giá trị lớn nhất là \(2AM\) \(\Leftrightarrow xy\perp AM\)

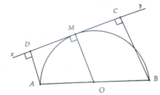
Ta có ABCD là hình thang vuông tại C và D
Mà O Là trung điểm AB và OM vuông góc với CD( tiếp tuyến của (O)
=> AD+BC=2OM=2R. Chú ý rằng CD ≤ AB (hình chiếu đường xiên)
=> S A B C D = 1 2 A D + B C . C D
= R.CD ≤ R.AB = 2 R 2
Do đó S A B C D lớn nhất khi CD=AB hay M là điểm chính giữa nửa đường tròn đường kính AB