Cần phải thiết kế các thùng dạng hình trụ có nắp đựng nước sạch có dung tích V c m 3 . Hỏi bán kính R c m của đáy hình trụ nhận giá trị nào sau đây để tiết kiệm vật liệu nhất?
A. R = 3 V 2 π 3
B. R = V π 3
C. R = V 4 π 3
D. R = V 2 π 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Đổi 20 lít =20000cm3.
Gọi bán kính nắp đậy của thùng sơn là x (cm), x>3,
chiều cao của thùng sơn là h(cm).
Khi đó thể tích của thùng sơn là

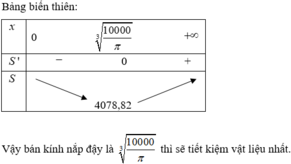

Đáp án B.
Gọi h(m) là chiều cao của chiếc bồn nước, h > 0 .
Thể tích của chiếc bồn là V = π r 2 h = 10 ⇒ h = 10 π r 2 .
Diện tích toàn phần của chiếc bồn là:
S t p = 2 π r 2 + 2 π r h = 2 π r 2 + 2 π r . 10 π r 2 = 2 π r 2 + 20 r = 2 π r 2 + 10 r + 10 r
Cách 1: Theo bất đẳng thức Côsi ta có: S t p ≥ 3 2 π r 2 . 10 r . 10 r 3 = 3. 200 π 3 .
Dấu “=” xảy ra khi
2 π r 2 = 10 r ⇔ r 3 = 5 π ⇔ r = 5 π 3
Vậy với r = 5 π 3 thì lượng inox được sử dụng để làm bồn nước là ít nhất.
Cách 2: Xét hàm số f r = 2 π r 2 + 20 r , r > 0 .
Ta có
f ' r = 4 π r − 20 r 2 = 4 π r 3 − 20 r 2 ; f ' r = 0 ⇔ 4 π r 3 − 20 = 0 ⇔ r 3 = 5 π ⇔ r = 5 π 3
Bảng biến thiên:
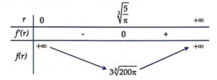
⇒ f r đạt giá trị nhỏ nhất tại r = 5 π 3 .

Đáp án C
Đổi 20 lít = 20 000 cm3
Gọi bán kính nắp đậy của thùng sơn là x (cm), x > 0, chiều cao của thùng sơn là h (cm)
Khi đó thể tích của thùng sơn là
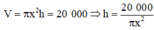
Diện tích toàn phần của thùng sơn là:
![]()
Để nhà sản xuất tiết kiệm được vật liệu nhất tức là Stp nhỏ nhất
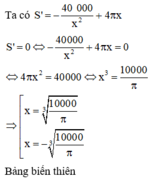
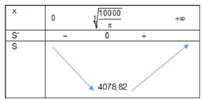
Vậy bán kính nắp đậy là 1000 π 3 thì sẽ tiết kiệm vật liệu nhất

Đáp án B
Yêu cầu bài toán “Tìm R để diện tích toàn phần của hình truh là nhỏ nhất”
Gọi h là chiều cao của hình trụ Thể tích khối trụ là V = π R 2 h = 10 ⇒ h = 10 π R 2 1
Diện tích toàn phần của hình trụ là: S T P = S x q + 2 × S d = 2 π R h + 2 π R 2 2
Từ (1); (2) suy ra S T P = 2 π R 2 + 20 R = 2 π R 2 + 10 R + 10 R ≥ 3 200 π 3
Dấu = xảy ra khi và chỉ khi 2 π R 2 = 10 R ⇔ R = 5 π 3 m
Đáp án là D
