Trong không gian với hệ tọa độ Oxyz, cho hai điểm A 1 ; 1 ; 0 , B 0 ; − 1 ; 2 . Biết rằng có hai mặt phẳng cùng đi qua hai điểm O, A và cùng cách B một khoảng bằng 3 . Vecto nào trong các vecto dưới đây là một vecto pháp tuyến của một trong hai mặt phẳng đó?
A. n 1 → = 1 ; − 1 ; − 1 .
B. n 2 → = 1 ; − 1 ; − 3 .
C. n 3 → = 1 ; − 1 ; 5 .
D. n 4 → = 1 ; − 1 ; − 5 .


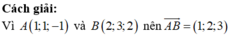

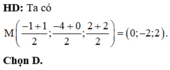

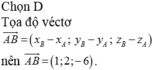

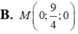
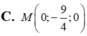


Đáp án D.
Phương pháp:
Gọi n → a ; b ; c , n → ≠ 0 → là một VTPT của α . Viết phương trình mặt phẳng α .
Sử dụng các giả thiết O ∈ α ; A ∈ α ; d B ; α = 3 lập hệ phương trình tìm a, b, c.
Cách giải:
Gọi n → a ; b ; c , n → ≠ 0 → là một VTPT của α .
O 0 ; 0 ; 0 ∈ α ⇒ α : a x + b y + c z = 0
A 1 ; 1 ; 0 ∈ α ⇒ a + b = 0 ⇒ b = − a ⇒ α : a x − a y + c z = 0
d B ; α = 3 ⇔ a .0 − a . − 1 + 2 c 2 a 2 + c 2 = 3 ⇔ a + 2 c 2 a 2 + c 2 = 3
⇔ a + 2 c 2 = 3 2 a 2 + c 2 ⇔ a 2 + 4 a c + 4 c 2 = 6 a 2 + 3 c 2 ⇔ 5 a 2 − 4 a c − c 2 = 0
Cho
a = 1 ⇒ c 2 + 4 c − 5 = 0 ⇔ c = 1 c = − 5 ⇒ n → 1 ; − 1 ; 1
hoặc n → 1 ; − 1 ; − 5 .