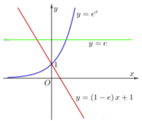
Cho H là hình phẳng giới hạn bởi các đồ thị hàm số y = e , y = e x và y = 1 − e x + 1 (tham khảo hình vẽ). Diện tích của H là
A. S = e + 1 2
B. S = e + 3 2
C. S = e − 1 2
D. S = e + 1 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình hoành độ giao điểm của đồ thị f(x) và g(x) là
![]()
![]()
Do đồ thị của hai hàm số cắt nhau tại ba điểm suy ra phương trình (*) có ba nghiệm là -3;-1;1
Ta được ![]()
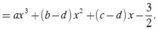
Đồng nhất hai vế ta suy ra ![]()
Vậy diện tích hình phẳng cần tìm là 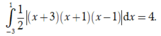
Chọn A.

Đáp án D
Hoành độ giao điểm của (H) và (d) là nghiệm: x − 1 x + 2 = − 2 x − 4 ⇔ x = − 1 x = − 7 2
Hoành độ giao điểm của (d) và Δ là nghiệm: 2 = − 2 x − 4 ⇔ x = − 3
Hoành độ giao điểm của (H) và Δ là nghiệm: x − 1 x + 2 = 2 ⇔ x = − 5
Khi đó, diện tích hình phẳng cần tính là S = ∫ − 5 − 7 2 x − 1 x + 2 − 2 d x + ∫ − 7 2 − 3 − 2 x − 4 − 2 d x = − 5 4 + 3 ln 2
Đáp án A
Xét hệ giao điểm:
y = e y = 1 − e x + 1 ⇔ y = e x = − 1
Xét hệ giao điểm:
y = e x x = e ⇔ x = 1 y = e
Dựa vào hình vẽ ta có:
S = ∫ − 1 0 e − 1 − e x − 1 d x + ∫ 0 1 e − e x d x
= ∫ − 1 0 e − 1 x + 1 d x + e x − e x 0 1 = e − 1 x 2 2 + x − 1 0 + 1 = 1 2 e − 1 + 1 = 1 2 e + 1