Cho hai đường thẳng song song Δ 1 và ∆ 2 . Nếu trên hai đường thẳng Δ 1 và ∆ 2 có tất cả 2018 điểm thì số tam giác lớn nhất có thể tạo ra từ 2018 điểm này là
A. 1020133294.
B. 1026225648.
C. 1023176448.
D. 1029280900.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Giả sử trên ![]() có
có ![]() điểm thì trên
điểm thì trên ![]() có
có ![]() điểm.
điểm.
Ta lấy 1 điểm trên ![]() và 2 điểm trên
và 2 điểm trên ![]() hoặc 2 điểm trên
hoặc 2 điểm trên ![]() và 1 điểm trên
và 1 điểm trên ![]() sẽ tạo thành 1 tam giác.
sẽ tạo thành 1 tam giác.
Do đó số tam giác tạo thành là ![]() .
.
Ta có
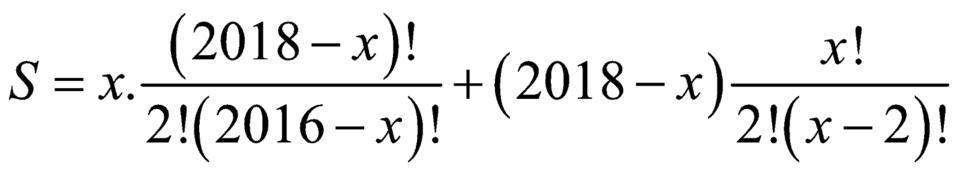
![]()
![]()
Biểu thức đạt giá trị lớn nhất khi ![]() .
.
Giá trị lớn nhất khi đó là ![]() .
.

a) Sai
Sửa lại: "Đường thẳng Δ là đường thẳng vuông góc chung của hai đường thẳng chéo nhau a và b nếu Δ cắt cả a và b, đồng thời Δ ⊥ a và Δ ⊥ b"
b) Đúng
c) Đúng
d) Sai
Sửa lại: Đường thẳng đi qua M trên a và vuông góc với a, đồng thời cắt b tại N và vuông góc với b thì đó là đường vuông góc chung của a và b.
e) Sai.

\(\Delta\) đi qua M(1,-1) có hệ số góc k
=> \(\Delta:y=k\left(x-1\right)-1=kx-k-1\)
\(\Delta\) song song d: \(y=\dfrac{1}{2}x+\dfrac{1}{2}\) \(=>k=\dfrac{1}{2}\)
\(\Delta:y=\dfrac{1}{2}x-\dfrac{3}{2}\)

a: (Δ)//d nên Δ: -x+2y+c=0
=>VTPT là (-1;2)
=>VTCP là (2;1)
PTTS là:
x=3+2t và y=1+t
b: (d): -x+2y+1=0
=>Δ: 2x+y+c=0
Thay x=4 và y=-2 vào Δ, ta được:
c+8-2=0
=>c=-6

Đáp án A
*Gọi (Q) là mặt phẳng chứa d và vuông góc với mặt phẳng (Oxy). Để khoảng cách giữa hai đường thẳng d và ∆ nhỏ nhất thì ∆ chính là giao tuyến của hai mặt phẳng (Oxy) và mp (Q).
* Mặt phẳng (Oxy) có phương trình là z = 0 có VTPT n Oxy → = (0; 0; 1).
Đường thẳng d đi qua A(1;2; -3) và có VTCP u d → = (1; -2; 0)
Suy ra, VTPT của (Q) là n Q → = [ u d → ; n Oxy → ] = (2; 1; 0)
Phương trình mặt phẳng (Q) là: 2(x - 1) + 1(y - 2) + 0(z + 3) = 0
Hay 2x + y -4 =0
* Đường thẳng ∆ cần tìm là giao tuyến của hai mặt phẳng (Oxy) và (Q). Tập hợp các điểm thuộc ∆ là nghiệm hệ phương trình: 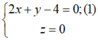
* Đặt x = 1 + t thay vào (1) ta được: y = 4 - 2x = 4 - 2(1 + t) = 2 - 2t
Suy ra, phương trình tham số của đường thẳng ∆ là: 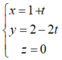
Đáp án là B