Cho lăng trụ đứng tam giác ABC A'B'C' có đáy là một tam giác vuông cân tại B, A B = B C = a , A A ' = a 2 , M là trung điểm BC Tính khoảng cách giữa hai đường thẳng A M v à B' C
A. a 7
B. a 3 2
C. 2 a 5
D. a 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
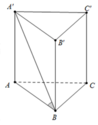
Ta có: S đ = B C 2 2 = a 2 2 Do A'B tạo (ABC) với một góc 60 ∘ nên A ' B A ⏜ = 60 ∘
Do đó
AA ' = A B tan 60 ∘ = a 3 ⇒ V A B C . A ' B ' C ' = S đ h = a 3 3 2 .

Đáp án A
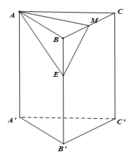
Gọi E là trung điểm của BB' => ME//B'C => (AME)//B'C
![]() = d(C;(AME))
= d(C;(AME))
Vì ![]()
![]()
Gọi h là khoảng cách từ B đến mặt phẳng (AME).
Do tứ diện BAME có BA, BM, BE đôi một vuông góc nên :
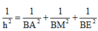
![]()
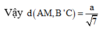

Đáp án D
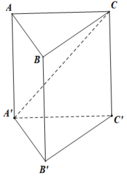
A ' C ; B C = A ' C ; A ' C ' = ∠ C A ' C ' = 30 0 C C ' = A ' C ' . tan 30 0 = 2 a 3 3 = 2 3 a 3 V A B C . A ' B ' C ' = C C ' . S A B C = 2 3 a 3 . 1 2 .2 a .2 a = 4 3 a 3 3


Đáp án B
Gọi H là hình chiếu của A lên A’B.
Khi đó d A ; A ' B C = A H
Ta có:
1 A H 2 = 1 A A ' 2 + 1 A B 2 = 1 2 a 2 + 1 a 2 = 5 4 a 2 ⇒ A H = 2 a 5

Đáp án D
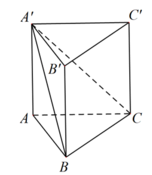
A ' B C , A B C = A ' B A ^ = 30 0 .
A A ' = A B . t a n 30 0 = a 3 3 .
S A B C = 1 2 B A . B C = a 2 2 2 .
V A B C = A A ' . S A B C = a 3 3 ⋅ a 2 2 2 = a 3 6 6 .

Đáp án D
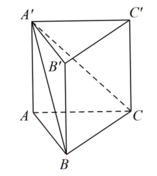
A ' B C , A B C = A ' B A ^ = 30 0 .
A A ' = A B . t a n 30 0 = a 3 3 .
S A B C = 1 2 B A . B C = a 2 2 2 .
V A B C = A A ' . S A B C = a 3 3 ⋅ a 2 2 2 = a 3 6 6 .

\(AC=\sqrt{10^2-6^2}=8\)
S đáy=1/2*6*8=3*8=24
V=24*5=120
Đáp án A
Gọi E là trung điểm của B B ' ⇒ M E / / B ' C ⇒ A M E / / B ' C
⇒ d A M ; B ' C = d B ' C ; A M E = d C ; A M E
Vì B C ∩ A M E = M , B M = M C ⇒ d C ; A M E = d B ; A M E
Gọi h là khoảng cách từ B đến mặt phẳng (AME).
Do tứ diện BAME có BA, BM, BE đôi một vuông góc nên
1 h 2 = 1 B A 2 + 1 B M 2 + 1 B E 2 = 1 a 2 + 4 a 2 + 2 a 2 = 7 a 2
Vậy d A M , B ' C = a 7